
 Chapter II
Chapter II 
HUMAN BEHAVIOR
Before one can even begin to account for behavior in terms of activities of the nervous system, one must have some idea of what behavior is. The early psychologists began by studying the mind or mental processes, but, in an attempt to put psychology on a more solid scientific footing, abandoned the study of the mind and concentrated on the study of behavior. In fact, most modern psychologists probably define psychology as the study of behavior. They define behavior as the "observable responses of an organism" (Kendler, 1963). In most modern psychology textbooks, the topic of mind is not even mentioned because the mind is not observable. A quick scan of the table of contents of such a text shows the following topics: sensation, perception, learning, motivation, talking, frustration, conflict, personality, social behavior, emotion, and abnormal behavior. It is surprising that movement is seldom discussed as a behavior per se.
Looking back over the list of topics in the preceding paragraph, it is striking how few of these behaviors are actually observable. Sensation and perception are not observable by anyone else except the person experiencing them. Learning, motivation, conflict, frustration, and emotion are also not observable; we merely infer their existence from the behavior of the person after they occur. A person says he has seen something. That is the behavior we observe; the talking of the person, not his sensation or perception. An animal's behavior changes in a training situation, and we infer that it has learned. What we observe are the consequences of learning, motivation, etc. Is it less reasonable to infer the other workings of the mind: thinking, calculating, and reasoning? We should not be surprised that a great deal of progress has not been made in understanding these phenomena; it is always more difficult to deal on a scientific basis with inferences or constructs than with directly observable events like movement. A thorough discussion of behavior would require several volumes, but a discussion of sensation and movement is presented as groundwork for later discussions of their neurophysiology.
| Psychophysics |
The scientific consideration of sensation began in the 1800s, when physicists and mathematicians began to wonder if a sensation could be treated like any other "physical" phenomenon. That is, they wondered, "Could sensation be quantified?" This early interest in sensation was the first step in the formation of neurophysiological understanding of sensation. The science of psychophysics was developed to determine just what can be sensed. Elaborate methods have been developed to measure sensation, but a detailed description of these methods is beyond the scope of this presentation. We will confine our discussion to what these methods tell us about sensation.
We all are aware of various aspects of our world through our senses. These senses are mediated by structures, called receptors, that are specialized to be particularly sensitive to some form of energy, either light, mechanical, thermal, or chemical energy. Eyes are receptors sensitive to light energy. Ears are receptors for mechanical energy in the form of sound vibrations and so on. Stimuli are simply presentations of energy to sensory receptors. One important aspect of a stimulus is its strength or intensity. Not every strength of a particular form of energy can be sensed by a human. The minimum strength required to cause a sensation is called the threshold(1) . Below this threshold level there is no sensation.
In Table ii-1 are listed some threshold values for various sensory modalities. The table will give you an idea of the exquisite sensitivity of our sensory receptors and the units used to specify thresholds. (The units of measure will be further dealt with when we consider each sense separately.) Take vision for example. The absolute threshold for many visual receptors (i.e., the minimum energy required to excite a visual receptor) is one photon, a single particle of light. (You may recall, light has properties of both waves and particles. Here it is useful to think of light as particles.) Now look at audition. The threshold for vibration of the eardrum, that is, the minimum distance the eardrum must move for a sound to be heard, has been estimated at 10-8 cm or about half the diameter of the hydrogen ion. Auditory systems are extremely sensitive to pressure vibrations in the air. Only the best man-made instruments approach the sensitivity of these that have developed in nature.
Table ii-1 | |
|---|---|
Thresholds for Some Stimuli in Various Modalities | |
Modality |
Threshold |
| Vision |
|
| Audition |
|
| Olfaction |
|
| Taste |
|
| Somesthesia |
|
The thresholds are listed in the table as if they were constants, but in fact they are only representative values. The actual threshold values depend upon three factors:
- the method used to measure them
- the individual being tested
- the environment in which the thresholds are measured
Some people are more sensitive than others to certain stimuli. Sensitivity often varies with age, and in women sensitivity can vary with time during the menstrual cycle. Distracting a subject's attention will elevate the threshold measured for any person by any method.
Although thresholds for sensation are useful in determining the minimum energy a person can respond to, they tell us little about the range of stimulus strengths we can sense. For example, what happens to our perception when the strength of a stimulus is increased by some amount? You might say, "That's simple, the magnitude of the sensation evoked increases," and in general, that's true if the increase in stimulus strength is great enough. But, if we expect to gain an understanding of the underlying physical mechanisms, we need more precise information. There are a number of ways that sensation can be related to stimulus strength. For instance, there could be a linear relationship between the amount of stimulus energy (S) and the sensation or, in psychological terms, the response (R), such that equal increments in stimulus strength yield equal increments in the magnitude of the sensation.
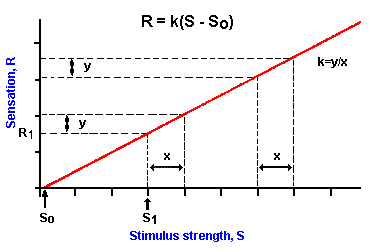 |
Fig. ii-1. A plot of a linear relationship between stimulus stength (S) and response magnitude (R) as expressed by the equation R=k(S-So) where So is the threshold stimulus strength. In a linear relationship, equal changes in stumulus strength (x) yield equal changes in response magnitude (y) no matter what the values of strength and magnitude. |
The graph of Figure ii-1 shows a linear relationship of the form
![]() R = k (S-So).
R = k (S-So).
R is the magnitude of the sensation plotted on the y-axis or ordinate. S is the stimulus strength plotted on the x-axis or abscissa. The term k is a constant, and it is the slope of the straight line. Its value can be computed by dividing the value y by the value x in the illustration. Notice that the line intercepts the abscissa at the value So. Because the abscissa corresponds to R = 0, that means that when S = So there is no sensation, i.e., R = 0. Notice that there is a range of stimulus values, S < So, that is not sensed. Therefore, So is the threshold value of the stimulus and is here treated as if it were a constant. Actually, the threshold is not a constant, as we have said. We therefore arbitrarily set the threshold at that value of stimulus strength that gives a sensation in 50% of its presentations. The magnitude of the sensation, R, evoked by any stimulus, S, that is above threshold, can be determined by reading up from the stimulus value on the abscissa to the corresponding point on the plot, then across to the ordinate. . Thus, the stimulus, S1, yields response, R1, in the figure. Notice that equal increments in stimulus strength, "x," produce equal increments in sensation, "y," no matter what the absolute values of S and R might be. This is the principal feature of a linear relationship. Changes in stimulus strength are accurately signaled over the whole range of strengths. The main disadvantage of a linear relationship is that only a relatively small range of strengths can be accommodated because of limitations on the maximum and minimum rates at which neurons can discharge. As we shall see, in many senses the advantage of linearity, namely, discriminability, has been sacrificed in order to sense a greater range of strengths.
Let us examine other possible relationships and see how one goes about testing whether a relationship between a stimulus and the resulting sensation is linear or non-linear. Let us compare the heaviness of two weights as our sample problem. One way to do the experiment is to put a weight into each of a subject's hands and ask whether one weight is heavier. Suppose we begin with two 100-gram weights. If the subject is normal, he will say that the weights are equally heavy. Now, add small amounts of weight to one hand until the subject can first discriminate that one weight is heavier than the other. We find that we need to add 2 grams. When the subject can first detect a difference, we call the difference between the two weights the just-noticeable-difference, or JND. We cannot measure sensation directly because it is covert and we cannot lay a ruler to it. We therefore must express equal increments in sensation in terms of the changes in stimulus energy that produce them. The JND is thus a standard unit of measure of sensation and represents, in actuality, the amount by which stimulus strength must be changed to produce a different sensation, an example of a difference threshold.
With a 100-gram weight, the JND was 2 grams. Expressed as a fraction, the ratio of the JND to the standard weight, S, is 2 divided by 100, or JND = 0.02. Now we repeat the experiment, starting with 150-gram weights in each hand. We find that the subject cannot detect a difference until three grams have been added. Now the JND is three grams instead of two as before. However, the ratio of the JND to the standard weight, that is, JND/S, is still 0.02 (3/150). No matter what standard is chosen, within limits, we find that the ratio JND/S = 0.02. This means that the amount of weight that must be added for the subject to detect a difference is a constant proportion of the standard weight--not a constant increment as the linear relationship would require. The ratio of JND to the standard is called the Weber fraction. It turns out that for most sensations, the Weber fraction is a constant (although not necessarily the same constant for different sensations) over a moderate range of intensities. However, at the upper and lower extremes of stimulus strength, the Weber fraction is no longer constant. Although this is of theoretical importance, it need not concern us at this point.
Table ii-2 | |||
|---|---|---|---|
Development of the Logarithmic Relation From the Weber Fractiona | |||
|
|
|
|
| 0 | 2 | 0.3010 | 0.0792 |
| 1 | 2.4 | 0.3802 | 0.0792 |
| 2 | 2.88 | 0.4594 | 0.0792 |
| 3 | 3.456 | 0.5386 | 0.0792 |
| 4 | 4.147 | 0.6178 | 0.0792 |
| 5 | 4.9764 | 0.6969 | 0.0792 |
| a JND=kS, k=0.2, So=2 | |||
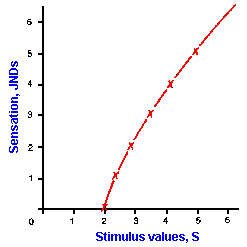 |
Fig. ii-2. The logarithmic relationship between stimulus strength and response magnitude. The sensation values are plotted against stimulus values in Table ii-2. |
Using the observations that for many of our senses there is a threshold stimulus strength below which we sense nothing and the ratio of the JND to the standard, S, is a constant, we can develop the law that relates sensation to stimulus strength (Table ii-2). For example, let us assume a threshold value of two and a Weber fraction (that is, the JND to S ratio) of 0.2. Because the Weber fraction is constant, we will use it as our basic measure. The table lists JND steps and the corresponding stimulus strengths for our example. The stimulus strength for each succeeding JND, the values for which are shown in the second column, was computed by multiplying the previous S value by the Weber fraction, 0.2, and adding it to the previous S value. Thus, from a standard value of 2 (the threshold), the stimulus must be increased by 0.4 units to 2.4 for a change in sensation to be perceived. With a standard of 2.4, the stimulus must be increased by 0.48 units to 2.88, and so on. When plotted, the values of JND versus stimulus strength yield the curve shown in Figure ii-2. If the logarithms of the stimulus values are compared as shown in the third column of the table, the differences between successive log values are the same, namely 0.0792. If we plot the JND versus log S instead of the JND versus the S value itself, we get a straight line of slope k. Figure 2-3 shows that this is true. The data from Figure ii-2 are replotted with the magnitude of the sensation again plotted on the ordinate. This time, however, we have plotted the logarithm of the stimulus values on the abscissa. A major feature of the logarithmic relationship is that each log unit represents an equal percentage (constant proportion) change in the value of S. Notice that equal changes in sensation, "y," are produced by equal percentage changes in strength, "x".
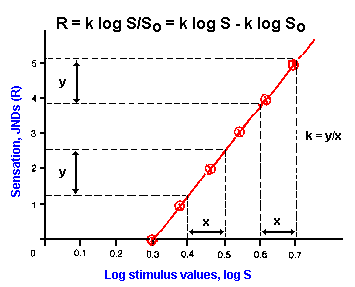 |
Fig. ii-3. Logarithmic relation. Data presented in Table ii- 2 are replotted, this time plotting the log stimulus values instead of the values themselves, yielding a linear relationship whose equation is R=k log (S/So). Notice that equal percentage changes in stimulus strength result in equal changes in response no matter what the values of strength and magnitude. |
A general relationship between stimulus strength and response magnitude for most senses then is the log function,
![]() R = k log (S/So),
R = k log (S/So),
where R is the magnitude of the response, S is the stimulus strength, k is a constant for the particular sense, and So is the threshold stimulus strength, again treated as if it were a constant. You can prove to yourself that So is indeed the threshold. Rearrange the basic equation to the form
![]() R = k log S - k log So.
R = k log S - k log So.
If So is the threshold, then when S = So, R should equal zero. The magnitude of the sensation is a linear function of the log of the stimulus strength. This log relationship is usually referred to as the Weber-Fechner function or simply the Fechner function.
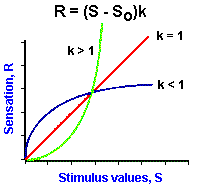 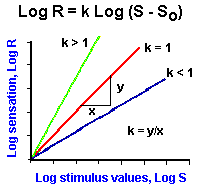 |
Fig. ii-4. Examples of power functions of the form, |
As mentioned earlier, the logarithmic relationship holds fairly well for midrange values of stimulus strength, but breaks down near threshold and maximal values. Because of this failure, the relationship between sensation and stimulus strength is often better fitted by a power function. With a power function, sensation is related to stimulus strength raised to some power. Mathematically, a power function is represented by the equation
![]() R = (S - So)k.
R = (S - So)k.
In Figure ii-4A are plotted three power functions with different powers or exponents. They are k is equal to 1, k less than 1 and k greater than 1. Notice that in the case of k = 1 the power function is a straight line, the lines are curved upward for powers greater than 1, and downward for powers less than 1. It should be pointed out that all three curves pass through the origin; thus, the threshold, So, is set at zero. However, this is usually not the case; So usually has some nonzero value! The power function R = (S-So)k can be rearranged to the form,
![]() log R = k log (S-So).
log R = k log (S-So).
This is the equation for a straight line. Therefore, if the values of sensation and stimulus intensity are plotted on log-log coordinates, a straight line results, and the slope of this line is the exponent k. The power function relationship says that equal percentage changes in stimulus strength give equal percentage changes in the magnitude of the sensation.
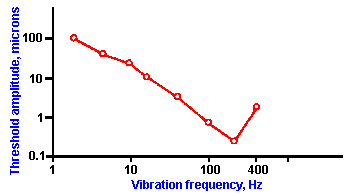 |
Fig. ii-5. The threshold displacement for vibration of the palm of the hand is plotted against the frequency of the vibration. (Mountcastle VB, LaMotte RH, Carli G: J Neurophysiol 35:122- 136, 1972) |
But what is the biological significance of these complicated relationships between sensation and stimulus? Why have organisms evolved in this way? We will demonstrate the biological significance of logarithmic and power relationships by use of an example. The average human can detect vibration of the palm of the hand over a range of frequencies from 2 to 400 cycles per second (or Hertz, Hz). A typical response curve is shown in Figure ii-5. In this graph, the amplitude of the vibration at threshold, expressed in micrometers, is plotted on the ordinate, and the frequency of the sine wave vibration stimulus, on the abscissa. The lowest threshold occurs at about 200 Hz, but the range of frequencies detected lies between 2 Hz and 400 Hz. With a standard frequency of 200 Hz, the measured JND for frequency of vibration is about one-tenth of the period or 0.5 msec (0.1 x 5 msec). This means that the period of the sine wave must be changed by 0.5 msec in order for the change in frequency to be detected. The 0.5-msec change in period corresponds to a 20-Hz change in terms of frequency. A frequency of 220 Hz is distinguishable from 200 Hz, but any frequency in between 220 and 200 Hz is not distinguishable from 200 Hz. A 2-Hz stimulus has a period of 500 msec, whereas the period of a 400-Hz stimulus is 2.5 msec. These periods differ by 497.5 msec, which is divisible into 995, 0.5-msec intervals.
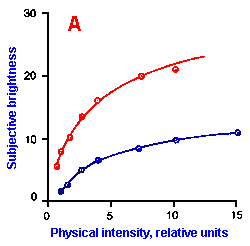 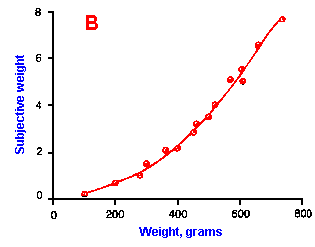 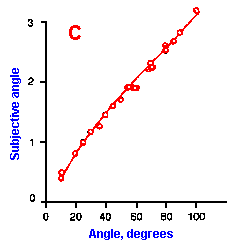 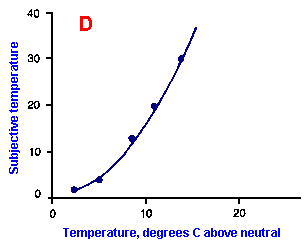 |
Fig. ii-6. Relationship between stimulus and response magnitudes for four sensations. Linear plots of stimulus magnitude (abscissa) against perceived magnitude (ordinate). A. Subjective brightness of lights of 672 nm (red) wavelength and 554 nm (green) wavelength at different strengths. B. Perceived magnitude of a lifted weight. C. Perceived angle between two surfaces felt with hands. (Ekman G: Some aspects of psychophysical research. In Rosenblith WA [ed}: Sensory Communication. Cambridge, MA, MIT Press, 1961) D. Geometric mean for 12 observers of perceived warmth of a stimulus applied to the inside of the forearm plotted against temperature in degrees centigrade above the threshold. (Stevens SS: The psychophysics of sensory function. In Rosenblith WA [ed]: Sensory Communication. Cambridge MA, MIT Press, 1961) |
If the sensation of vibration frequency were a linear function of period length over the whole range of frequencies, a subject could distinguish 995 different frequencies. We have seen that the nervous system deals in action potentials, tiny voltage changes that last 0.5 to 1 msec. If nerves from the skin were to signal a 2-Hz vibration by discharging 1 impulse/second, then the signal for 400 Hz would have to be nearly 1000 impulses/second. If each impulse lasts 1 msec, it is impossible for a neuron to squeeze more than 1000 impulses into a second. In actual fact, most neurons cannot discharge more than 400 to 500 impulses/second. This would create a problem for coding for the nervous system. However, the sensation of vibration frequency is not related directly to the stimulus period, but rather to a percentage of the period by the Weber fraction, JND/S = 0.1. Therefore, the number of frequencies that can actually be distinguished over the range from 2 to 400 Hz is only about 59, but the range of frequencies is greater than could be had by a linear relationship. A neuron discharging 1 impulse/second for a 2-Hz stimulus would only need to discharge 50 impulses/second to signal a 400-Hz vibration. This is an easy task for most neurons.
Thus, what the logarithmic or power relationship does is to expand the range of stimulus values that the person can sense, but the cost is a loss in ability to discriminate, usually at one end of the range of stimulus strengths or the other. This is made clear by examining the summary of the previous example in Table ii-3. If we limit the range of stimulus values by allowing only the values that can be signaled by a neuron (assuming an upper limit of 500/sec for axonal discharge rate), then the range of values a subject could sense if there were a linear function would be 2 to 4 Hz. (Remember the JND is expressed in periods, not frequencies! 500 msec - 500 intervals x 0.5 msec = 250 msec or 4 Hz.) The range for the logarithmic function would be 2 - 1.5 x 1023 Hz.
At the same time, the number of discriminable frequencies in the range of human perception would be 995 in the linear case and only 59 in the logarithmic case. On the average, the stimulus frequency must be changed by a greater amount to be judged as different in the case of a logarithmic or power relationship than would be the case if there were a linear relationship between sensation and stimulus strength. This is less true at lower frequencies than at higher ones. Of course, this analysis applies only to cases where the exponent of the power function is less than one. When the exponent is greater than one, sensitivity will be greater than for a linear relationship at the low stimulus strengths, but the range of stimulus values sensed is even smaller.
Table ii-3 | ||
|---|---|---|
Comparison of the Properties of Linear and Logarithmic Relations | ||
Property |
Linear
|
Logarithmic
|
| Range of stimulus values encodeable at 500/sec | 2-4 Hz | 2-1.5 x 1023 Hz |
| Number of discriminable frequencies in the range 2-400 Hz | 995 | 59 |
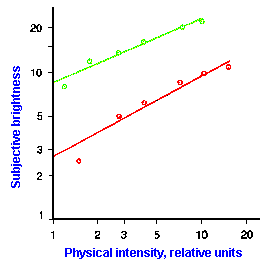 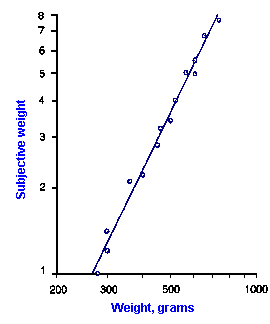 |
Fig. ii-7. Relationship between stimulus and response magnitude for two sensations. Log plots of stimulus magnitude (abscissa) against log perceived magnitude (ordinate) for brightness and weight perception in fig. ii-6. |
So far, we have dealt mainly with abstractions, but now we can examine some concrete examples of sensory thresholds. Linear plots of stimulus-response relationships for various sensations are shown in Figure ii-6. Upward concaved plots are shown for the perceived weight of a lifted object (B) and sensations of warmth (D). Downward concaved relations are shown for subjective brightness of lights of 554 nm (green, upper curve in A) and 672 nm (red, lower curve) and perceived angle between two surfaces felt with the hands (C). Figure ii-7 shows log-log plots for the two of the sensations included in Figure ii-6. Notice that the curves that are concaved upward result in lines with slopes greater than one (B), whereas those that are concaved downward result in lines with slopes less than one (A). The exponents of the power functions fitted to these data are 0.363 (red) and 0.356 (green) for brightness curves, 1.6 for perceived weight, 0.28 for perceived angle, and 1.6 for warmth.
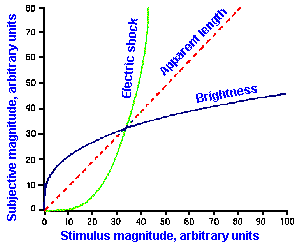
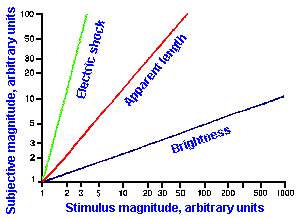
Other examples of stimulus-response relationships are shown in Figure ii-8. In A are shown on the same linear axes, relationships between subjective magnitudes and stimulus magnitudes for sensitivity to electrical shock, visually estimated length, and brightness. These are concave upward (electric shock), concave downward (brightness), and nearly linear (apparent length). The resulting exponents of the descriptive power functions are 3.5 for shock, 0.33 for brightness, and 1.4 for length. These are the slopes of the lines in Figure ii-8B that are log-log replots of the data in A.
Exponent values for power functions for various sensory experiences, varying over a fairly wide range, are summarized in Table ii-4. The lowest value in the table is 0.28, the highest 3.5. Most values are near 1.0, i.e., nearly, but not quite linear. Different exponent values are sometimes obtained for the same variables, the exact value depending upon how the experiment is conducted and, therefore, the exact sensitivity measured. For example, when the magnitudes of sensations evoked by electrical shocks are measured using 60-Hz alternating current, the relationship is a simple power function with an exponent of 3.5, as shown in Figure ii-8. On the other hand, when single electrical pulses are used instead of alternating current, the relationship is a double power function, one extending from 0 to 2 mA with exponent 1.8 and one extending from 2 to 50 mA with exponent 0.9. Probably, two different sensations are being measured in these two studies. We will see, when we consider the sensory modalities, how some of these psychophysical functions may be related to processes in the central nervous system.
|
Fig. ii-8. Relationship between stimulus and response magnitudes for electric shock, visually estimated length, and brightness. A. Linear plot of stimulus strength (abscissa) versus response magnitude (ordinate). B. Log-log replot of data in A. (Stevens SS: The psychophysics of sensory function. In Rosenblith WA [ed]: Sensory Communication. Cambridge MA. MIT Press, 1961) |
Let us summarize our discussion of psychophysics. Psychophysics is the science of measuring sensations and their thresholds. Thresholds vary depending upon the method of measurement and the individual. The magnitude of sensation increases as the stimulus energy is increased. The just-noticeable-difference is the amount of increase in stimulus strength needed in order for a person to perceive that a change has occurred. For most sensations, the JND is a constant fraction of the standard of comparison over a moderate range of stimulus values. Finally, the relationship between the magnitude of a sensation and the stimulus strength most often is a power function. This allows a greater range of stimulus strengths to be sensed, but decreases the discriminability of two different stimulus strengths at low powers and a greater discriminability with a smaller range at high powers.
Table ii-4 | ||
|---|---|---|
Representative Exponents of Power Functions Relating
| ||
Sensation |
Exponent |
Stimulus Conditions |
| Loudness | 0.6 | Binaural |
| Loudness | 0.54 | Monaural |
| Brightness | 0.33 | 5 target - dark-adapted eye |
| Brightness | 0.5 | Reflectance of gray paper |
| Saturation | 1.2 | Point source - dark-adapted eye |
| Smell | 0.55 | Coffee odor |
| Smell | 0.6 | Heptane, citric acid |
| Taste | 0.8 | Saccharin |
| Taste | 1.3 | Sucrose |
| Taste | 1.3 | Salt |
| Temperature | 1.0 | Cold - on arm |
| Temperature | 1.6 | Warmth - on arm |
| Vibration | 0.95 | 60 Hz - on finger |
| Vibration | 0.64 | 250 Hz - on finger |
| Duration | 1.1 | White-noise stimulus |
| Repetition rate | 1.0 | Light, sound, touch, shocks |
| Angleb | 0.28 | Felt angles |
| Length | 1.4 | Visual estimation of line length |
| Finger span | 1.3 | Thickness of wood blocks |
| Pressure | 1.1 | Static force on skin of palm |
| Weightb | 1.6 | Lifted weights |
| Heaviness | 1.45 | Lifted weights |
| Force of handgrip | 1.7 | Precision hand dynamometer |
| Autophonic level | 1.1 | Sound pressure of vocalization |
| Painc | 0.9 | Electrical shocks to tooth pulp |
| Electrical shock | 3.5 | 60 Hz, through fingers |
| Electrical shocksd | 1.8, 0.9 | Single pulses |
| a All values from Stevens SS: The psychophysics of sensory function. In Rosenblith WA [ed]: Sensory
Communication. Cambridge, MA, MIT Press, 1961.
b Ekman G: Some aspects of psychophysical research. In Rosenblith, WA [ed]: Sensory Communication. Cambridge, MA, MIT Press, 1961. c Schwartz P: J exp Psychol 45:288-293, 1953. d Rosner PS, Giff WR: Contrib Sensory Physiol 2:169-221, 1968. | ||
| Movement |
The range of movements that a human can produce is really extraordinary. He or she can move both rapidly and with great endurance, attaining speeds of 10 m/sec over a distance of 100 m. Amongst animals this is not a speed record by any measure; there are animals both faster and slower. The swift (a bird) is capable of speeds of 62 m/sec through the air, and the cheetah of 29 m/sec over land. Yet, although a man cannot outrun an antelope or kangaroo in a short distance (antelopes and kangaroos are capable of speeds of 18 m/sec for short distances), Australian aborigines are able to run them down over long distances. Modern man is capable of running nonstop more than 180 miles at an average speed of 2.7 m/sec (6 miles per hour). In water a human can achieve a speed of 2 m/sec for short distances (100 meters). He can jump into the air more than 2 meters and leap at the end of a run nearly 9 meters; he can throw a hammer more than 75 meters (250 feet) and lift over his head more than 236 kg (521 pounds, McWhirter N: Guinness Book of World Records. New York, Sterling, 1979).
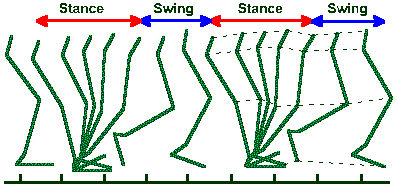 |
Fig. ii-9. Stick figures representing lower limb of a normal man walking on level ground at a rate of 90 steps/min. Approximate boundary positions for stance and swing phases are indicated. (Brunnstrom S: Clinical Kinesiology, 3rd ed. Philadelphia, FA Davis, 1972) |
Obviously, these movements were achieved by athletes or highly practiced individuals and, therefore, they are not representative of the abilities of the average human. Figure ii-9 shows a movement of the average human, two complete stepping cycles in a normal man walking at the rate of 90 steps/min. Stepping is divisible into two phases: a stance phase and a swing phase, both of which are indicated in the figure. The stance phase begins when the heel of the foot hits the ground (footfall) and ends when the toe is removed again, whereas the swing phase begins when the toe leaves the ground and ends when the heel makes contact again. Propulsion in the forward direction is achieved near the beginning of the stance phase when the joints of the limb are extending. The force they exert upon the substrate is not applied exactly vertically but obliquely, the horizontal component producing forward movement.
Figure ii-10 shows the rotation of the hip, knee, and ankle joints during the first cycle of stepping after a subject is given a "go" signal. Shortly after the signal, the toe leaves the ground and the ankle, hip, and knee joints are all flexing, as the leg is lifted. Before the end of the swing phase, the ankle and the knee begin to extend in preparation for contact of the limb with the ground, whereas the hip joint remains flexed until well into the stance phase, when it begins to extend as the leg moves backward with respect to the body. Just after the beginning of the stance phase, the ankle begins to flex as the leg begins its backward movement, and finally it extends again, lifting the heel away from the ground. The knee does not begin to flex again until the heel is removed from the ground, at which time the ankle and hip begin to extend. The three joints do not move in phase; the ankle leads the knee; the knee leads the hip. The pattern of movement in Figure ii-10 occurs in all normal people.
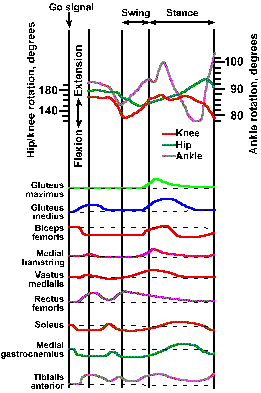 |
Fig. ii-10. Rotation of joints and muscle contraction during the stepping cycle in man. Upper: Angular motion of the ankle, knee and hip joints during the step cycle. All movements are calibrated from a standard anatomic position: hip and knee at 180 degrees and ankle at 90 degrees. The subject began stepping at the "go" signal. Swing and stance phases are marked; circled numerals indicate: 1. beginning of ankle rotation, 2. foot flat on ground, 3. heel off, and 4. toe off. Lower: Envelope of the EMG activity of various muscles of the limb during the stepping cycle. Dashed lines indicate baseline EMG activity. (Herman R, Cook T, Cozzens B et al.: Control of postural reactions in man. In Stein RB, Person KG, Smith RS, et al. [eds}: Control of Posture and Locomotion. Advances in Behavioral Biology, Vol. 7. New York, Plenum Press, 1973) |
The durations of the swing and stance phase vary with the speed of stepping, but the duration of the stance phase is always longer than the swing phase. As the stepping speed increases, the duration of the stance phase decreases, but the duration of the swing phase stays about the same, of the order of 0.5 sec, still remaining shorter than the stance phase. The two limbs move such that the toe of one limb leaves the ground, beginning its swing phase, when the center of mass of the body is nearly directly over the other foot, at the foot flat position. The hip and shoulder on the same side of the body move out of phase, such that when the hip is extending, the shoulder is flexing. The contralateral shoulder moves in phase with the hip.
The swing phase begins with increased activity in the gluteus medius, rectus femoris, and tibialis anterior muscles and decreased activity in the biceps femoris, soleus, and medial gastrocnemius muscles, as shown at the bottom of Figure ii-10. In the trace beside the name of each muscle, an upward deflection indicates an increase in the activity of the muscle, and a downward deflection indicates a decrease. The decrease in activity of the soleus and medial gastrocnemius occurs suddenly 130-210 msec after the go signal and leads the increased activity in the antagonistic muscles (muscles with opposite action at the same joint) by 20-60 msec. Just before the beginning of the stance phase, all of the muscles whose activity is shown in the figure begin to increase their activity, that is, all but the rectus femoris that is decreasing its activity. Most muscles have more than one period of activity or inactivity during a single stepping cycle. In fact, an increase or decrease in the activity of the gastrocnemius and soleus and the reciprocal decrease or increase in the activity of their antagonist, the tibialis anterior, occurs four times during the time from quiet stance to toe off. The reciprocal relationship between activities in antagonistic muscles is necessary to allow the joints to rotate. We will see later that much is known about the neurophysiology of the stepping cycle, but much still remains to be learned about how the stepping cycle is initiated and how it is modified to compensate for differences in terrain or for the presence of obstacles. We are also beginning to get a picture of what goes on in the nervous system during simple movements of the arms and basic locomotion (see Chapter 16), but of more complicated movements, such as playing the piano, we know little.
Psychologists treat movements as if they were all responses to stimuli and therefore individual, isolatable units. This results from the stimulus-response paradigms of the behaviorist's theoretical framework and appears to be related to the insistence that behavior be observable. But, not all behavior is observable; animals and people do things that are unseen and can only be inferred from their later behavior. The author is reminded of a story told to him by Dr. Arnold Towe of the University of Washington. During a visit to the San Diego Zoo, Dr. Towe was watching the orangutan, who was lounging with his feet up and his head resting in his hands, much like an executive behind a desk. The orangutan was gazing about him but appeared to be paying no particular attention to another man smoking a cigar, standing near Dr. Towe. The orangutan got up and began walking slowly around the cage in a spiral path that eventually brought him near the man with the cigar. When he was near enough, the orangutan's hand shot out, and he grabbed the cigar before the man could react. The orangutan then resumed his "executive" posture, this time smoking the cigar as he had observed the man doing. Clearly, the orangutan had been paying careful attention to what was happening around him, but this attention was not observable and therefore, for the psychologist, could serve as neither stimulus nor response.
This example also serves to illustrate that behavior is not a series of disjoint stimuli and the responses to them. Rather, it is a continuous flow system in which stimuli are constantly present and changing, and behavior is continuous and continuously modifiable by both changing stimuli and previous behavior. This conceptual framework has made little impact on the thinking of physiologists, perhaps because we do not have an adequate way of dealing with flow systems in our thought processes.
| Other behaviors |
A simple catalog of human behaviors would fill several volumes, but even simple ones like perception and movement are not easily explained, as we shall see. More complex behaviors pose another type of problem for both the psychologist and the physiologist--that is the problem of definition. What do we mean by emotion, motivation, personality or frustration? What is thinking? Do animals do it? If so, how can we tell when they are doing it? Until we can get adequate answers to these questions, it is doubtful that any real progress can be made towards understanding these behaviors. Still, some progress has been made, as we shall see in Chapter 17.
| Suggested Reading |
- Herman R, Cook T, Cozzens B, Freedman W: Control of postural reactions in man. In Stein RB, Pearson KG, Smith RS, Redford JB [ed]: Control of Posture and Locomotion. Advances in Behavioral Biology, Vol. 7. New York, Plenum Press, 1973.
- Herman R, Wirta R, Bampton S, Finley FR: Human solutions for locomotion. I. Single limb analysis. In Herman RM, Grillner S, Stein PSG, Stuart DG [ed]: Neural Control of Locomotion. Advances in Behavioral Biology, Vol. 18. New York, Plenum Press, 1976.
- Kendler HH: Basic Psychology. New York, Appleton-Century-Crofts, 1963.
- McWhirter H: Guinness Book of World Records. New York, Sterling, 1979.
- Stevens SS: Psychophysics, New York, John Wiley, 1975.
Footnotes:
1. The term "threshold" may cause some confusion because of its multiple usages in the field of neurophysiology. We will use the term threshold in the sense defined above. To refer to the minimum change in stimulus strength required to elicit a different sensation, we will employ the term "difference threshold" or its psychological equivalent "difference limen." Do not confuse these concepts with the level of depolarization from the resting membrane potential at which the action potential is initiated. We will refer to this as the "critical firing level."
[TOC] [Chapter 1] [Glossary] [Index] [Abbreviations]
This page was updated: July 17, 2011.
