Chapter 3
Chapter 3 
PROPERTIES OF EXCITABLE MEMBRANES:
THE SPIKE
| The action potential or spike |
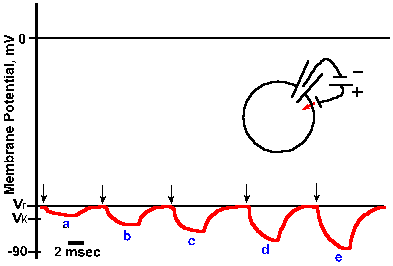 |
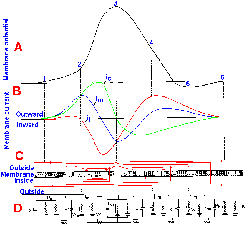
Fig. 3-15. Changes in membrane potential caused by inward current flow. Five equal 4-msec steps of inward transmembrane current, with current magnitude increasing from a to e, resulted in five proportional hyperpolarizing changes in membrane potential. Responses reflect simple electrotonic potentials. |
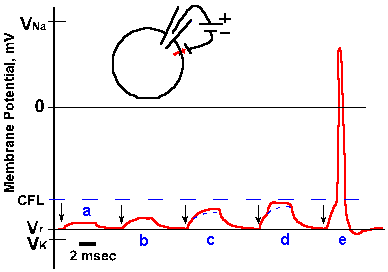 |
Fig. 3-16. Changes in membrane potential due to outward current flow. Five equal 4-msec steps of outward transmembrane current, with current magnitude increasing from a to e (and the same magnitudes as for similarly lettered traces in Fig. 3-15), resulted in hypopolarizing electrotonic potentials in a and b, electrotonic potentials leading to local active responses (region between solid and dashed lines) in c and d, and an electrotonic potential leading to a spike in e. CFL=critical firing level. |
When a still stronger current is passed outward through the membrane, the membrane potential begins to change passively (Fig. 3-16 e); then the active process begins; and finally the membrane polarization continues to diminish rapidly toward zero (the membrane is hypopolarized), and it even becomes positive inside with respect to outside. The membrane polarity actually becomes reversed. After the peak of positivity is reached, the membrane rapidly returns to its original polarity and potential and may proceed to a potential more negative than Vr. Finally, the membrane returns to Vr, the whole event lasting 2-3 msec. Actually, the event, from its start at Vr to peak positivity and back to Vr (omitting the period when Vm is more negative than Vr), requires only 0.5-1.0 msec, depending upon the neuron. This event is called the action potential or simply the spike.
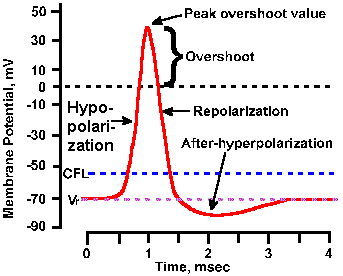 |
Fig. 3-17. Phases of the action potential. The time course of the spike is shown with hypopolarization (depolarization) and repolarization phases, overshoot, and hyperpolarizing and hypopolarizing after-potentials labeled. Also indicated are levels of the resting membrane potential, Vr, and the critical firing level, CFL. Transmembrane voltage is indicated on the ordinate; time is indicated on the abscissa. |
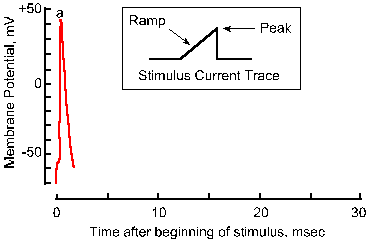 |
Fig. 3-18a. Accommodation of the nerve membrane. Response to a single pulse of current with a very fast rise-time. |
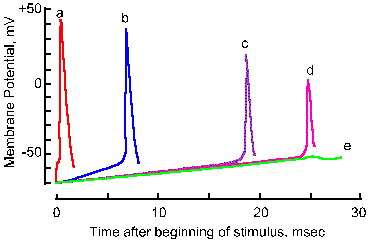 |
Fig. 3-18b. Accommodation of the nerve membrane. Five superimposed traces show the membrane response to linearly varing electrical stimuli with rates of rise decreasing from a to e. Note that the critical firing level changes from a 21-mV hypopolarization in a to a 28-mV hypopolarization in d, and no spike occurs in e. Note also that the amplitude of the spike falls with decreasing rate of rise (Frankenhaeuser and Vallbo, Acta Physiol Scand 63:1-20, 1965). |
The action potential is initiated when the membrane is hypopolarized beyond a certain value. This value, termed the critical firing level (CFL), varies from cell to cell; it is of the order of 10-20 mV, but constant for a given cell under its normal working conditions. The critical firing level is a highly unstable condition. If the membrane is hypopolarized just to but not beyond the critical firing level, it may either discharge a spike or it may simply return to Vr.
Actually, a minimum rate of change in membrane potential is required to initiate the spike. If the membrane potential is changed very slowly, the critical firing level can be passed without an action potential being initiated. In Figure 3-18, the responses of an axon to stimuli with five different rates of rise are shown. As the rate is decreased (going from a to e), the apparent critical firing level becomes more positive, going from 21 mV of hypopolarization from Vr in a to 28 mV in d. In e, no spike is initiated at all, in spite of the fact that the membrane is hypopolarized by more than 30 mV. Actually, during any maintained hypopolarization that does not cause a spike to occur, the critical firing level becomes more positive. This phenomenon is called accommodation. When the hypopolarization is terminated, both the membrane potential and the critical firing level return to their original values. If, however, the minimum rate of change of membrane potential is exceeded, the spike will be initiated as the membrane potential becomes more positive than the critical firing level. Most neural events are rapid, and it is doubtful the firing level is ever crossed in natural functioning of the healthy neuron without a spike occurring. There are certain pathological conditions where this occurs, e.g., in certain kinds of epileptic seizures where there are extremely large changes in membrane potentials at synaptic junctions.
| The critical firing level is the level beyond which the membrane must be hypopolarized to initiate a spike. |
Once the action potential is initiated, it goes to completion. The maximum value of the positive overshoot is a constant (usually about +30 mV) for a given neuron when the spike is initiated starting with the membrane at or near Vr. The amplitude of the spike does not depend upon the size of the stimulus; larger stimuli do not give rise to larger spikes. Longer duration stimuli do not prolong spikes. Therefore, the spike is referred to as an all-or-none (often written all-or-nothing) event. The fixed size results from the fact that the stimulus only triggers events that lead to the spike; once they are triggered their time-course is independent of the stimulus. The consequences of slowly rising stimuli producing accommodation (Fig. 3-18) are an apparent contradiction to this all-or-none property; but, as pointed out above, most naturally-occurring changes in membrane potential occur rapidly at rates higher than 4 mV/msec, at which the spike amplitude is reduced by less than 2%.
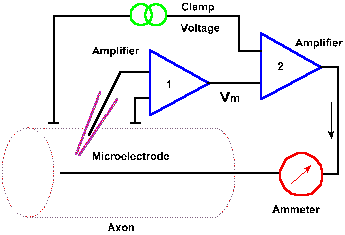 |
Fig. 3-19. Circuit diagram for the voltage clamp. Transmembrane potential is measured between an intracellular micropipette electrode and an electrode in the extracellular fluid by amplifier 1 and compared with the clamp voltage by amplifier 2. A current (downward arrow) is generated to bring the membrane potential to the clamp voltage, and the current is measured by the ammeter. |
The voltage clamp
What are the events that lead to the action potential? Obviously, the change in membrane potential of the spike results from a membrane current, and that current must result from an increase in membrane conductance. If membrane conductance were unchanged, there would be no disturbance of the resting membrane equilibrium. Membrane currents can be measured directly using a device called the voltage clamp. The circuit of the voltage clamp is shown in Figure 3-19. The membrane potential of the squid axon or another cell is measured with a micropipette as in previous figures, using amplifier 1. The output of this amplifier is compared, by a second amplifier, with a command signal specified by the experimenter. The command signal indicates the voltage at which the membrane is to be "clamped," the clamp voltage. If the membrane potential is not the same as the command signal, a current is generated by the second amplifier that is appropriate in magnitude and direction to bring the membrane potential to the clamp voltage. If, in the neuron, a current is generated that would result in a change in membrane potential, that change is sensed and countered as it occurs by the voltage clamp. In this way, the membrane potential is maintained at the clamp voltage. The current that is generated by the second amplifier, the clamp current, is measured by the ammeter. This current will be equal in magnitude, but opposite in direction to any membrane current.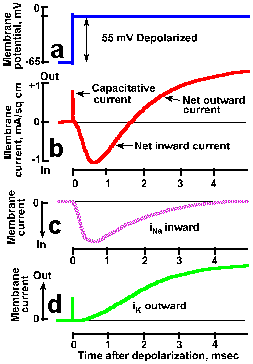 |
Fig. 3-20. Transmembrane currents during a spike. A. The transmembrane potential showing rapid clamp at -10 mV from a resting potential of -65 mV, a 55-mV hypopolarizaton. B. Total membrane current consists of a brief capacitative current, lasting only a few microseconds, a slower net inward current (downward deflection of the trace is inward current by convention) lasting about 1.5 msec, and a prolonged outward current. Total ionic current can be divided into two components: a transient inward current caused by sodium entry (C) and a prolonged outward current caused by potassium efflux (D). (Hodgkin and Huxley, J Physiol (Lond)116:449-472, 1952). |
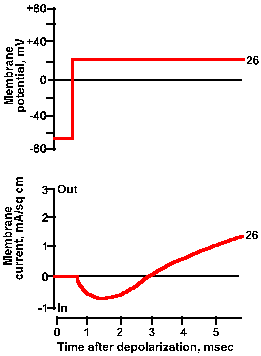 |
Fig. 3-21a. Effect of membrane potential on membrane current. Upper trace shows +26 mV clamp voltage; lower trance shows total net current current for this clamp voltage. |
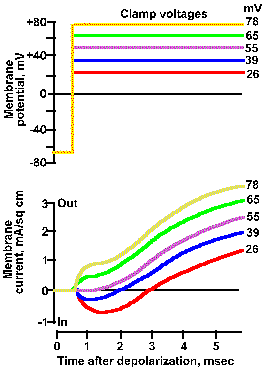 |
Fig. 3-21b. Effect of membrane potential on membrane current. Upper traces show five different clamp voltage, +26 to +78 mV, applied to the squid axon. Lower trances show total net current flows for each clamp voltage. As the clamp voltage becomes more positive, the net outward current becomes larger and larger, whereas the net inward current becomes smaller, is zero at 52 mV, and then becomes net outward (Hodgkin, Huxley and Katz, J Physiol (Lond) 116:424-448, 1952). |
There are a number of ways to determine which ions are carrying the currents. First, suppose that the concentration of Na+ in the extracellular fluid is reduced, and Na+ is replaced by choline, such that VNa+ = -10 mV. Then, when the membrane potential is clamped at -10 mV, Vm = VNa+ and
![]() iNa+ = gNa+(Vm - VNa+) = 0.
iNa+ = gNa+(Vm - VNa+) = 0.
Therefore, there will be no current due to sodium ions. The resultant voltage-clamp current is shown in Figure3-20d as a smoothly rising outward current. The inward current is eliminated completely, suggesting that it was carried by sodium ions. Another way to show this is to vary the clamp voltage in an axon with normal ion concentrations. The result of doing this is shown in Figure 3-21. When the membrane is clamped at +26 mV, the inward current is reduced but present, and the outward current is larger than that at a clamp voltage of -10 mV. At a clamp voltage of +39 mV, the inward current is still smaller and the outward current still larger, whereas, at +52 mV (approximately VNa+), the inward current is eliminated completely. This is what would be expected if the inward current is carried by Na+ because at +52 mV, Vm = VNa+ and thus iNa+ = 0. When the membrane potential is clamped at +65 or +70 mV, an outward current appears where the inward current used to be, again as expected.
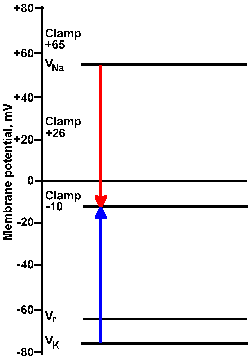 |
Fig. 3-22a. Driving force diagram. With the membrane voltage clamped at -10 mV, the driving force on K+ is proportional to the length of the arrow from VK+ to the clamp -10 line at the left of the figure. The driving force on sodium is proportional to the length of the arrow from VNa+ to the clamp -10 line. Directions of the forces are given by the direction of the arrows, upward being outwardly directed, downward, inwardly directed. |
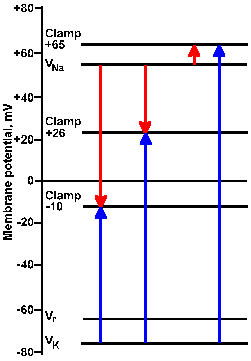 |
Fig. 3-22b. Driving force diagram. The center pair of arrows show driving forces on K+ and Na+ at a clamp voltage of +26 mV, whereas the right pair shows them for a clamp voltage of +65 mV. Note that all K+ driving forces are outward; sodium driving forces are inward for -10 and +26 mV, and outward for +65 mV. |
Consider the driving force diagram of Figure 3-22. In this diagram, Vr, VNa+, and VK+ are indicated along with the clamp voltages -10, +26, and +65 mV. Recall that the driving force on an ion is Vm - Vion. Therefore, at a clamp voltage of -10 mV (Vm), the driving force on Na+ is equal to the length of the line (downward arrow) in the driving force diagram from VNa+ to the -10 mV clamp voltage. Likewise, the driving force on K+ is the length of the line from VK+ to the -10 mV clamp voltage (upward arrow). In both cases, the direction of the arrowhead indicates the direction of the driving force and the direction of the current flow that results from it, inward for Na+, outward for K+. (The arrow in the driving force diagram indicates the direction of current flow. A cation will move in that direction; an anion will move in the opposite direction.) If the sodium conductance increases, there will be an inward iNa+; if gK+ increases, there will be an outward iK+.
| The arrow in a driving force diagram indicates the direction of current flow. A cation will move in that direction; an anion will move in the opposite direction. |
The magnitudes and directions of the driving forces for both Na+ and K+ are similarly indicated by the lengths and directions of the lines to the +26 and +65 mV clamp voltages. Notice that the driving force for K+ is greater as the clamp voltage becomes more positive, and it is always directed outward. We should, therefore, expect the magnitude of the outward current, if it is carried by potassium ions, to become larger as the membrane potential is clamped at more and more positive values. This is seen clearly in Figure 3-21.
The driving force for Na+ decreases as the clamp voltage approaches VNa+. When the clamp voltage is more positive than VNa+, the driving force reverses direction from toward the inside to toward the outside of the membrane. At even more positive values of the clamp voltage, the driving force will increase in magnitude, but its direction will still be outward. At clamp voltages less positive than VNa+, iNa+ will be an inward current; at values more positive it will be an outward current, again as seen in Figure 3-21.
We can show that the outward current in Figure 3-20 is a potassium current in a similar way. If the extracellular K+ concentration is increased such that VK+ is equal to the clamp voltage, there is no outward current, only inward current (shown in Figure 3-20C), the sodium current. The sodium current can also be calculated by subtracting the potassium current in Figure 3-20d from the total current in Figure 3-20b. To make this calculation, it is necessary to assume that there is no interaction between Na+ and K+ ions or their conductances. This is probably a good assumption, because, as we shall see, the conductances for the two ions change at different times during the action potential, and the outward and inward currents can be blocked independently. Tetrodotoxin (TTX), a toxic substance that occurs naturally in the puffer fish(12), blocks the inward sodium current and, with it, the action potential, without changing the outward potassium current. The lethality of TTX is due to its ability to block sodium action potentials. The behavior of TTX contrasts sharply with that of tetraethylammonium (TEA); TEA ions block the outward K+ current without influencing the sodium current.
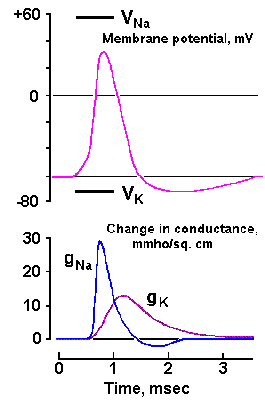 |
Fig. 3-23. Changes in sodium and potassium conductances during the spike in the squid axon. Upper trace shows the time course of the spike. Lower traces show the earlier rapid increase in gNa+ from near 0 to 30 mS/cm2 and the slower return to near zero and the delayed, slower increase in gK+ to more than 10 mS/cm2, followed by a slower return to resting levels (Aidley: The Physiology of Excitable Cells. Cambridge: Cambridge Univ. Press, 1971). |
Activation and inactivation
What causes the increase in gNa+ during the action potential? The answer is, the initial hypopolarization! How? Recall that some of the membrane proteins act as channels or pores through which lipid-insoluble substances can pass. Actually, three types of channels are recognized. Some channels, e.g., some K+ channels, are open all the time and allow ions to pass through the membrane down their electrochemical gradients. Many K+ channels are open in the resting membrane, but few Na+ channels are. Other channels are gated, some electrically and some chemically. Chemically gated channels are opened by substances called transmitter substances, and they occur in specialized regions of cells where contacts are made with other cells (i.e., at synapses). We will have more to say about them later.The voltage-gated channels are opened when the membrane is hypopolarized. Because the cell membrane is so thin, the resting potential sets up an electric field across the membrane that has a strength of about 100 kV/cm of membrane thickness. The Na+ channel, and perhaps similarly the K+ channel, is a single glyco-polypeptide of molecular weight 260,000-300,000 (at least, the one in Electrophorus electricus, an electric fish). The molecule is estimated to be 29% carbohydrate, and it consists of four homologous domains, each composed of 6 segments. The molecule must be elaborately folded, with some portions making up the channel itself and others comprising either intra- or extracellular appendages (for a possible structure see Guy and Seetharamulu: Proc Nat Acad Sci 83: 508-512, 1986). The diameter of the channel is estimated at about 0.8 nm. The charged groups within the channel give it a large electric dipole moment, and the dipoles tend to align themselves with the electric field in such a way as to close the channel. Field strength is altered by hypopolarization, according to a popular hypothesis, causing the dipoles to reorient and open the channel. At any rate, the channel is opened by hypopolarization, allowing Na+ to enter the cell, which it does because of its concentration gradient. Sodium entry holds the channel open longer and causes more channels to open, allowing more sodium to enter and more channels to open, etc. Opening of the channel is called activation.
Until recently, it has been impossible to study the behavior of ion channels because the currents that flow through them are so small, a few picoamps, that noise in the recording system completely hid the small signals. However, a new recording technique, called the patch-clamp, allows the opening and closing of single channels to be studied. Briefly, the patch-clamp technique involves pressing a polished micropipette electrode against the cell membrane and applying a bit a negative pressure to the lumen of the pipette. If all goes well, the orifice of the pipette seals against the membrane with sufficient strength that little current can pass between the membrane and the pipette edge, and the pipette can be withdrawn and actually rip-off the piece of membrane covering the orifice. The seal formed ensures that currents passing through the membrane patch will flow into the pipette and be recorded.
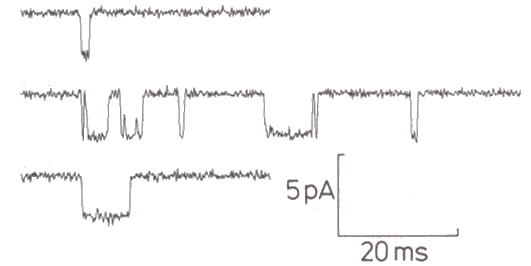 |
Figure 3-24. Sample channel activity. Channel is closed with trace is "up," open when trace is "down." From Sigworth, FJ. Chapter 14 in Sakmann and Neher Single-channel Recording, New York: Plenum1985, 309. |
Using this technique, we now know that ion channels open and close so quickly that transitions cannot be resolved, i.e., the current pulses appear to be rectangular. Channels appear to open in an all-or-none fashion, each increasing conductance by about 8 x 10-12 siemens, although changes in conductance vary from channel to channel(13). There have been some reports of channels with two open states, but most appear to have only one. In general, increasing the amount of hypopolarization or, for chemically gated channels the amount of transmitter substance, does not increase the size or duration of the currents that flow when a channel opens, but rather decreases the time between openings, i.e., it increases the probability of the channel being open. Also, the channels appear to open independently, i.e., the opening of one channel is not influenced by the condition of other channels in the same membrane. The patch-clamp technique has also shown that there is a vast array of types of ionic channels in different types of cells. Fortunately, at our level of analysis, we need not concern ourselves with most of them.
Once sodium channels are opened, something causes them to close again. This is called inactivation. The channels do not, however, go back to their original closed state. The inactivated channel cannot be reopened until the membrane repolarizes and the channel returns to the resting, closed condition, and Na+ conductance during inactivation is even lower than in the resting membrane. The membrane potential has to remain at a value more negative than the critical firing level for a msec or so before the channel can be opened again. This accounts for the phenomenon of accommodation: As the membrane is hypopolarized by a small amount, less than the critical firing level, some Na+ channels open and then (after a brief time) are inactivated, but not enough are opened to generate a spike. More and more channels are opened as long as the hypopolarization is maintained, but the rate of opening is still too low to lead to a spike and no channels are allowed to return to the closed, openable state. Once a channel is inactivated, it remains inactivated until the membrane repolarizes. If the rate of hypopolarization is slow enough, many of the Na+ channels can be inactivated without causing a spike, and the critical firing level will be pushed in the positive direction. When most of the channels have been inactivated, no spike can be initiated no matter how positive the membrane potential becomes.
| Sodium channels are opened by membrane hypopolarization, and they close after a certain time has elapsed. |
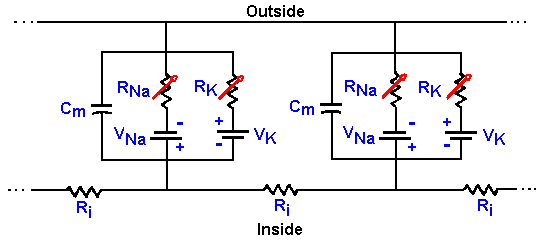 |
Fig. 3-25. Membrane equivalent circuit. The circuit of Fig. 3-14 redrawn to show that conductances (resistances) for sodium and potassium are not fixed, but variable. |
The ionic mechanism of the action potential
How then can we account for the action potential? First, we must update Figure 3-14 to include the variability of the Na+ and K+ resistances or conductances. In Figure 3-25, the fixed resistors are replaced with variable resistors, as indicated by the arrows through the resistor symbols. With this change, we can understand the mechanism of generation of the action potential. Initially, before the stimulus is applied to the neuron, gK+ is small, but gNa+ is much smaller, so Vr is near VK+. The stimulus or, as we shall see, an approaching action potential, provides an outward current that passively discharges the membrane capacitance, causing an hypopolarization of the membrane. As the membrane is hypopolarized, the sodium conductance rises as voltage-gated channels open, allowing some sodium ions to enter the cell down their electrochemical gradient, an inward current. The inward current (this is now active membrane) results in further hypopolarization, further increase in conductance as more voltage-gated channels open, and further entry of Na+ ions. This cycle of hypopolarization and increased conductance is sometimes called the Hodgkin cycle, and it is schematized in Figure 3-26. The result of this regenerative cycle is that the sodium battery is relatively much more important than the potassium battery in determining the membrane potential, Vm. Perhaps recalling the discussion of the circuits in Figure 3-7 will help to understand how the membrane potential can change so drastically with only a change in membrane conductance (gNa+). As the sodium battery makes itself felt, the membrane potential moves rapidly toward VNa+. If nothing changed at this point, gNa+ remained high and gK+ remained low, the membrane would seek a new resting potential predictable from equation 5 and near VNa+. But now, the inactivation begins; Na+ channels close (inactivate) and gNa+ drops. At the same time, the hypopolarization of the membrane has increased gK+ by opening voltage-gated K+ channels. Figure 3-26 shows that this process is not a regenerative one--increased hypopolarization leads to increased gK+, but increased gK+ leads to repolarization not hypopolarization. Any change in conductance with a change in voltage is a rectification(14). The change in gK+ is often called delayed rectification because it occurs at a later time than the change in gNa+. As gNa+ decreases and gK+ increases, the potassium battery again becomes relatively more important in determining the membrane potential, and so the potential falls back toward VK+. This repolarization further reduces Na+, and the change in potential accelerates. The potassium conductance does not inactivate as the sodium conductance does; it simply decreases with repolarization. This ensures that the repolarization occurs completely. Actually, the membrane would repolarize even if the sodium conductance inactivated and potassium conductance remained at resting levels, but the repolarization would take longer. The purpose of the increased potassium is to accelerate the repolarization and shorten the action potential. The potassium conductance also begins to decrease as the membrane repolarizes, but K+/gNa+ is greater than in resting membrane, so the membrane potential passes the resting level and moves even nearer to VK+ (hyperpolarizing afterpotential). Finally, as gK+ falls back to resting levels, the membrane potential moves back toward Vr as determined by equation 5.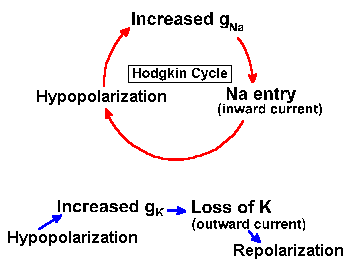 |
Fig. 3-26. Effects of increasing membrane conductance on the membrane potential. Hypopolarization leads to increased gNa+, which leads to sodium entry, which reinforces hypopolarization in the Hodgkin cycle (above), whereas hypopolarization leads to increased gK+, which leads to K+ efflux, which leads to repolarization (below). |
| The value of the resting potential depends strongly on the potassium equilibrium potential, weakly on the sodium equilibrium potential. The value of the peak overshoot potential is the reverse. |
Movements of ions during the spike
If there is a significant ionic current during the spike, ion concentrations both inside and outside the neuron should change. Actually, the ionic shifts through the membrane during the spike are small in relation to the intracellular and extracellular ion concentrations. Measurements of ion movements show that there is a net influx of about 3.7 x 10-12 moles of Na+ ions/cm2 of membrane and an equal K+ efflux during the spike. In large axons, this is about 1/1,000,000 of the resting concentrations. Even in small neurons, the actual ion movement is only 1/1000 of the resting concentration. There is, therefore, only a small change in ion concentration as a result of ion movement during the spike, a change that would not be measurable using ordinary chemical techniques, at least for large cells.The sodium ions that flow in are expelled by the sodium pump, which works not only to maintain resting ion concentrations, but also to restore these concentrations when they are disturbed. Actually, the sodium pump is not important for the individual spike because thousands of spikes can still be initiated in an axon in which the sodium pump has been poisoned with ouabain, cyanide, or dinitrophenol. It is required for long-term maintenance of excitability.
| The Upstroke of the action potential is due to Na+ entering the cell, the downstroke is accelerated by K+ leaving. |
Propagation of the action potential
Obviously, neurons must be able to generate action potentials without an experimenter passing current through the membrane. We will see later how sensory stimuli and synaptic transmission from other cells can lead to action potentials; it suffices for now to say that both types of stimuli eventually result in generation of a current outward through the membrane and an hypopolarization as described earlier. But, the outward current that results in a spike can also be generated by a spike occurring in an adjacent region of membrane.Because of Kirchhoff's law (current flows only in complete circuits), the current that flows into the cell during the upstroke of the action potential must flow along the inside of the cell and out through adjacent membrane as shown in Figure 3-27. This outward current flows through passive membrane, discharges the capacitance of the adjacent membrane, leading to an hypopolarization, an increase in gNa+, and an action potential. Once the inward ionic current of the spike is started, an outward current will be generated through the next segment of membrane(15). This process will be repeated in each adjacent segment of membrane throughout the length of the membrane, that is, the action potential will be propagated essentially without decrement along the membrane. The spike itself is an active process, due to the sodium battery, but propagation results from electrotonic (decremental) conduction (a passive process) into nearby membrane segments where a new spike is initiated. Each new spike has the same amplitude, so conduction occurs without decrement. This is equivalent to what the booster stations do along the transatlantic telephone cables.
| How can you tell if a membrane is "active" or "passive?" If the membrane conductance is the resting conductance, it's passive. If the conductance has changed, it's active. |
If the action potential is initiated in the middle of a length of axon membrane, it will propagate in both directions away from the site of initiation. We shall see later that conduction does not normally occur in both directions along an axon, but it can and this fact is used in stimulation of the dorsal columns to treat pain (see Chapter 6).
One result of propagation is that the action potential pattern as seen plotted in time in Figures 3-17 and 3-23 can just as well be plotted in length along the membrane as shown in Figure 3-27. The spike, shown in the upper panel, A, has been stopped instantaneously in space as it was traveling from right to left. In Figure 3-26 B are shown the total membrane current, im, the capacitative current, ic, and the ionic portion of the current, ii. Obviously, im = ic + ii. The total membrane current is indicated schematically through a section of membrane in C, where arrowheads indicate the direction of current flow, and the closeness of the lines indicates the approximate current density. In D, the equivalent circuit is shown with directions and approximate magnitudes of the membrane, capacitative, and ionic currents indicated by arrows. The changes in conductances are indicated by changes in the lengths of the Na+ and K+ resistance symbols.
Reading from left to right, successive segments of membrane are going through successive phases of the action potential at a given instant in time. Thus, at the time the spike was "frozen" in this position, it had not yet begun at site 1, but outward current (being driven by the inward current at site 3 and nearby) has begun to discharge the membrane capacitance. At site 2, the membrane is hypopolarized, increasing gNa+, and, therefore, iNa+. Between sites 1 and 2 the membrane current is mainly capacitative and outwardly directed, but between sites 2 and 3 the ionic current becomes larger as the Na+ channels open (Fig. 3-27B). The increased Na+ conductance is indicated by the shorter resistance symbol at site 2 than at site 1, and at site 3 than at site 2 in D. The sodium conductance has reached its maximum at site 3, and the potassium conductance has increased somewhat (as indicated by the shorter K+ resistance symbol in D) at the peak overshoot potential or the spike. The capacitative current is zero at site 3 because dV/dt = 0 and thus, im = ii.
Sodium inactivation is well underway, but potassium conductance is still high during the repolarization phase at site 4. Total membrane current is small and outwardly directed. Sodium inactivation is complete (as indicated by the long Na+ resistance symbol in D), but potassium conductance is still higher than normal causing the membrane potential to approach the equilibrium potential for potassium and generating the hyperpolarizing afterpotential at site 5. Both sodium and potassium conductances are normal and the membrane is back at the resting potential at site 6. Thus, the sequence of events occurring along the length of the membrane at an instant in time during conduction is exactly the same as that occurring in time at a fixed point on the membrane. You can view an animation of this process by clicking the picture at the right.
| The spike itself is an active process, due to the sodium battery, but propagation results from electrotonic conduction into nearby membrane segments where a new spike is initiated--a passive process. |
The velocity of the propagation of the spike increases with the magnitude of iNa+ or with the amount of the Na+ influx. The more current there is available to hypopolarize adjacent, unexcited membrane after local capacitance is discharged, the faster the adjacent membrane will hypopolarize to critical firing level and the faster it will generate current to hypopolarize unexcited membrane next to it, and so on. In order to hypopolarize adjacent regions of membrane, the inward iNa+ must traverse a volume of intracellular fluid. The resistance of that fluid is a factor in determining how much current actually reaches the adjacent membrane. The resistance to passage of current along the inside of the fiber decreases with the square of the inside fiber diameter; a larger area contains a larger number of potential current pathways. Thus, larger axons will have lower values of Ri and therefore have faster conduction velocities than smaller axons.
It is in propagation, nearly without decrement, that the reason for the existence of the action potential lies. The subthreshold events, that is, the events that occur in response to stimuli that do not bring the membrane to the critical firing level, are not propagated along the axon, but conduct decrementally. Events like those in Figure 3-15 and Figure 3-16a-d will produce no effect on the membrane of the cell at a distance of more than a few millimeters. The action potential will be of the same magnitude at the site of initiation and at the end of the cell, a meter or even several meters away. When it is necessary to communicate information (neural information) over distances greater than a few hundred micrometers, only the action potential will suffice.
Saltatory conduction
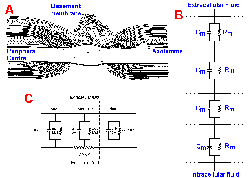
The ionic current that flows inward through the membrane results from an active process, the change in sodium conductance. On the other hand, the longitudinal current flow inside and outside the axon is passive, following the rules of electrotonic conduction. If the electrotonic potentials rise faster, i.e., if the time constant of the membrane, tau, is decreased, and if they decline less with distance, i.e., if the space constant, lambda, is increased, the conduction velocity must increase because more current will flow through more distant segments of membrane. The membrane time constant will decrease if the membrane capacitance is reduced, and the space constant will increase if the membrane resistance is increased.During evolution, animals first exploited increasing axon diameter as a means of increasing conduction velocity, but there is a limit to how large neurons can be; the problem is simply one of bulk. Few giant axons could be accommodated by the squid's body, unless it were greatly enlarged. Fortunately for the squid, it does not need many. The problem becomes even more severe when the nervous system contains more than 109 rapidly conducting neurons, as does the human nervous system. Another solution, which uses the principles of electrotonic conduction, requires the cooperation between neurons and glia, the Schwann cells in the peripheral nervous system and oligodendrocytes in the central nervous system (CNS). During development, the Schwann cells and oligodendrocytes wrap themselves around the axons, producing a fatty sheath, composed of layers of membrane and called myelin. Axons with a myelin sheath are said to be myelinated axons; axons without a myelin sheath are called unmyelinated axons. Each Schwann cell covers (totally surrounds) an area of membrane about 1 mm in length, with a space between adjacent Schwann cells, called the node of Ranvier or simply the node. The region of myelin coverage between two nodes is the internode. Figure 3-28A shows a node (with two adjacent segments of internode) in the peripheral nervous system (above) and the CNS (below). The central node is apparently more open to extracellular fluid, but the peripheral node is also bathed in extracellular fluid.
| Saltatory conduction occurs in myeli- nated axons because the action potential must jump over the internodes from node to node. |
The tightly wrapped layers of membrane prevent contact of extracellular fluid with the axon membrane in the internode, but such contact is provided at the nodes. Stacked Schwann cell membranes in the internode act as series resistances and capacitances as shown in Figure 3-28B. Because resistances in series are simply additive, the total resistance across the membrane and myelin at any point along the internode will be much higher than at any point along unmyelinated membrane or in the node of myelinated axons. Because series capacitances add as reciprocals, the transverse capacitance per unit area at any point along the internode will be much lower than at any point in the node. Measurements in the frog axon show that the resistance of the node is only 20 ohm-cm2, whereas that at the internode is 160,000 ohm-cm2. Conversely, the capacitance of the node is 3 microFarads/cm2, whereas the internode has a capacitance of 0.0025 microFarads/cm2. For a 12-micrometer axon, the node has an area of 20 micrometers2; the internode has an area of 88 x 103 micrometers2. Using these areas, the capacitance of a node and internode can be calculated (Fig. 3-28C). The calculated capacitance of the node is 0.6 picoFarads (pF), that of the internode 2 pF (recall that the area of the internode is much larger). At the same time, the measured transverse membrane resistance at the node is 80 megohms, that of the internode is 200 megohms, and the internal longitudinal resistance, Ri, is only 20 megohms.
Because the internode's membrane resistance is so high, most of the longitudinal current generated by a spike occurring at a node will pass along the intracellular fluid rather than outward through the myelin. Although there will still be some loss of electrotonic potential along the internode, the high resistance and low capacitance ensure that the loss will be less than in the same length of unmyelinated axon. The result is that most of the current will flow out through the nodes adjacent to the one with the ongoing spike, and the current density there will be high, sufficiently high to discharge the membrane capacitance rapidly to the critical firing level, initiating a spike. No action potential can occur in the internode, so the spike jumps from node to node to node. The conduction in myelinated axons is called saltatory (from the Latin, to jump). The current density at the node is about 20 mA/cm2 (current density in unmyelinated squid axon is seldom greater than 1 mA/cm2 under the same conditions), and this is 5-7 times greater than that required to bring the membrane to the critical firing level. This safety factor ensures that conduction from node to node will occur. In fact, saltatory conduction probably occurs between every other node or even every third node because there is sufficient current to bring to the critical firing level even the second or third node away from that where a spike is occurring.
Conduction in myelinated axons is much faster than in unmyelinated axons because the spike, at one point on the membrane, initiates another spike at a point further down the axon (1 or 2 nodes away) by virtue of the longer space constant. The largest unmyelinated fibers in mammals are 2 micrometers in diameter and conduct at 2 m/sec; the largest myelinated fibers are 22 micrometers in diameter and conduct at 120 m/sec. Longitudinal, intracellular resistance decreases as the square of internal diameter in myelinated as in unmyelinated axons, so conduction velocity in larger myelinated axons will be higher than in smaller ones. In peripheral nerves, a rough rule of thumb is that conduction velocity of myelinated axons in m/sec is six times the axon diameter expressed in micrometers. This estimate does not work well for axons in the central nervous system.
Refractory periods
Note in Figure 3-27 that current flows outward through the membrane both in front of and behind the advancing action potential. What prevents the action potential from turning around and propagating in the reverse direction? The answer lies in the refractory period. After the peak overshoot of the spike, the Na+ conductance begins to be inactivated, and, by the time the membrane repolarizes to the resting potential, sodium conductance is almost entirely inactivated. Recall that the membrane must remain near the resting potential for sometime (a millisecond of so) before the sodium channels return to their closed state, ready for activation again. During this time, the sodium conductance cannot be changed substantially by hypopolarization. Thus, a new spike cannot be initiated no matter how large the hypopolarization. This phase of inexcitability, called the absolute refractory period, is shown in Figure 3-28. It has about the same duration as the spike itself in many cells.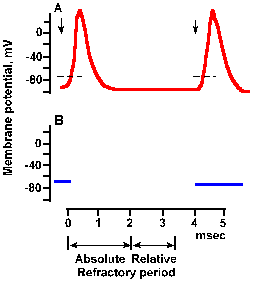 |
Fig. 3-29a. Time course of refractoriness following a spike. A. Spikes elicited by pairs of stimuli at a long time interval. The first stimulus was applied at the leftmost downward arrow. Because pairs are far apart in time, the response to this stimulus always has the same configuration. The second stimlus of the pair occurred 4 msec after the first. The is long enough for the refractory periods to have expired, and the spike is of normal configuration. |
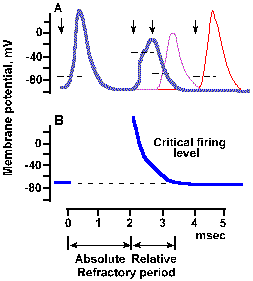 |
Fig. 3-29b. Time course of refractoriness following a spike. The second stimulus of the first par occurred 2 msec after the first stimulus (second arrow), of the second pair occurred about 2.8 msec after the first (third arrow), and (as in a) of the third pair occurred 4 msec after the first (fourth arrow). Spikes initiated during the refractory period are stunted and prolonged. Dashed line on rising phase of each spike indicates approximate critical firing level. B. Time course of change in critical firing level through the refractory periods. Approximate durations of absolute and relative refractory periods are indicated at the bottom of the figure (Dudel, in Schmidt RF, Fundamentals of Neurophysiology, 2nd ed. New York: Springer-Verlag, 1978). |
The refractory periods, absolute and relative, have two important consequences. First, the refractory period is long enough that the electrotonic and ionic voltages behind the spike have declined to below the critical firing level before the refractory period is over. Thus, the spike cannot turn around and go the other way. Likewise, because two action potentials cannot occupy the same region of membrane at the same time, two action potentials approaching each other along an axon will cancel each other out; neither action potential will pass the point of their meeting. This is called occlusion.
Another consequence of the refractory periods is that there is a maximum rate of discharge for the neuron. This rate is limited by the absolute refractory period for strong stimulation and by the relative refractory period for weak stimulation. A neuron that fires a 0.5-msec duration spike with a 1.0 msec refractory period cannot, under any circumstance, fire at a frequency greater than 1000/sec. If the spike and the refractory period are longer, the maximum frequency decreases.
| The spike itself is an active process, due to the sodium battery, but propagation results from electrotonic conduction into nearby membrane segments where a new spike is initiated--a passive process. |
Influences of other ions
Other ions, beside Na+ and K+, do not seem to play a major role in generation of the action potential, at least in axons like the squid giant axon. That is not to say that they cannot affect the action potential, however. Calcium has a complex effect on the action potential threshold. When the extracellular concentration of calcium is lowered, the axon becomes more sensitive to excitation, lowering the threshold for intracellular stimulation and causing the cells to discharge spikes spontaneously. The influence of calcium seems to be to stabilize the membrane. In some cases, muscle twitches occur when serum calcium levels are low; they cease when the person drinks some milk. This probably reflects this dependence upon calcium.At very low concentration of Ca2+, less than 1 x 10-5M, the axon becomes inexcitable by any stimulus intensity, although excitability can be restored by increasing extracellular Ca2+ again. Above-normal extracellular calcium concentrations depress neuron firing at many places in the central nervous system, yet they do not change either resting membrane potentials or membrane resistance. Synaptic potentials, the potentials that occur as a part of transmission between cells, are not influenced by increasing extracellular Ca2+. Magnesium ions have an influence on axon excitability similar to that of calcium, but, as we shall see, magnesium's effect on synaptic transmission is opposite to that of calcium.
Ok, why does this occur? It could be that the effect of mild reduction in Ca2+ is explained by supposing that Ca2+ is a voltage sensor--a gating particle that moves in the electric field of the membrane. It binds to a channel component at rest, keeping the pore closed, and it is pulled off the channel by membrane hypopolarization, opening the channel. The less calcium there is in the medium, the more channels are open and the lower the threshold (CFL). At even lower Ca2+ levels, the membrane may become excessively leaky to many small molecules, making the cell inexcitable. One explanation for the effect of increased Ca2+ concentrations is that Ca2+ is absorbed to the outer edge of the membrane, creating an electric field inside the membrane which adds to that provided by the resting potential. This would be equivalent to a membrane hypopolarization, so channels would open and stay open. If channels do not close, they cannot be reopened. Keep in mind that this is still speculative.
Neurons and muscles in mammals use sodium and potassium conductance changes to generate action potentials, but these are not the only ions that can serve this function. In fact, in crustacean muscles and in the dendrites and, in some cases, somata of neurons in the cerebral cortex, of Purkinje cells of the cerebellar cortex, of neurons in the inferior olivary nucleus, and perhaps of spinal motoneurons in mammals, Ca2+ takes the place of Na+ in carrying inward current. Calcium conductance is activated by hypopolarization, but the kinetics of activation are slower than those for sodium and thus the calcium spike develops more slowly and it lasts longer. Like the sodium conductance, the calcium conductance inactivates with time and potassium conductance increases, repolarizing the membrane. The calcium spike is not blocked by tetrodotoxin as is the sodium spike. Likewise, procaine, which blocks sodium spikes, is without effect on calcium spikes. Tetraethylammonium ions prolong and increase the amplitude of the calcium spike as they do for the sodium spike. The calcium spike is blocked (by competitive inhibition) by other divalent ions, Mn2+, Cd2+, Ni2+, but the sodium spike is not. This implies that, although Ca2+ can pass through Na+ channels, it has its own channels in membranes sustaining calcium spikes.
It has been noted that sodium spikes are found where rapid conduction of the action potential is important. Surely, the conduction velocity of the calcium spike would be slow; a definite speed advantage would lie with the sodium spike. On the other hand, in primitive, slowly moving animals, there was no particular premium on speedy conduction; calcium spikes probably sufficed. Calcium spikes are found when electrical excitation couples to an effector process, for example, muscle contraction or glandular secretion. The role of calcium spikes in the dendrites of neurons in the central nervous system is not known. It has been suggested that these calcium spikes are a holdover from more primitive times; yet there is no compelling evidence for this conjecture.
| Inhomogeneity of the nerve membrane |
We have seen that the axon membrane contains an abundance of voltage-gated sodium and potassium channels, giving it the ability to generate action potentials. The density of such channels in axons has been estimated at 1000 per micrometer2. Membranes that do not contain voltage-gated channels do not generate spikes. The soma and dendrites of some neurons have few, if any, voltage-gated channels, although neurons that support dendritic and somatic sodium or calcium spikes may have many. The receptor sites on membranes, sites sensitive to sensory stimuli and transmitter substances, do not generate spikes, but they do support non-propagated, graded potentials that lead to spikes. As we shall see, the generation of spikes in such membranes would disrupt their ability to encode the qualities of the stimulus.
The dendrites and soma have many chemically-gated channels, especially at the sites of contact with other cells at synapses. Some estimates indicate the number of such channels at synapses is limited only by their maximum packing density. Chemically-gated channels are of numerous types that can be classified either in terms of the chemical transmitter substance that opens them or in terms of their selectivity for certain ions. Some chemically-gated channels are opened by acetylcholine, others by norepinephrine and others by other substances. (For a further discussion of the topic of transmitter substances, see Chapter 13). Channels are seldom absolutely selective. Thus, the acetylcholine-gated channels at the neuromuscular junction, the synapse between the motoneuron and the muscle, allow both sodium and potassium ions, in fact, nearly all ions to pass through. This non-selective change in membrane permeability leads to an hypopolarization of the muscle membrane, the endplate potential, a spike, and muscle contraction. At other synapses, the channels open to create a more selective change in membrane conductance for potassium and chloride. Axons themselves contain no chemically-gated channels, except at sites of special synaptic contacts, the axoaxonic and nodal synapses.
| Different kinds of channels are found in different parts of neurons. That's why the parts behave differently. |
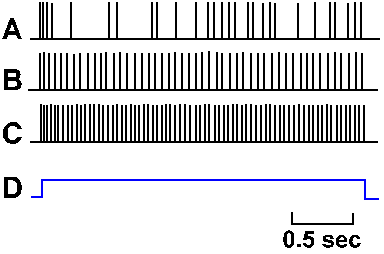 |
Fig. 3-30. Accommodation in the soma. A-C. Intracellularly recorded responses of a motoneuron to prolonged hypopolarizing current at increasing strength. A: 7 x 10-9 A, B: 7.7 x 10-9 A; C: 10 x 10-9 A. Upper trace of each pair shows action potentials generated by current; lower trace is the monitor of current flow; upward deflection is on (Granit, Kernell and Shortess, J Physiol (Lond) 168:911-931, 1963). |
Not only is the density of different kinds of ionic channels different in various parts of the nerve membrane, but the behavior of the sodium channel is different in different parts of the membrane. If a pair of micropipette electrodes is used to penetrate the cell body of a neuron as in Figure 3-8 and a constant current is passed outward through the membrane, a train of action potentials will be initiated, lasting as long as the current is maintained. Figure 3-30 shows this for three different magnitudes of current through the soma of a motoneuron. The monitor of the current, shown in the lower trace of each pair, turns on abruptly as the trace deflects upward and off abruptly as the trace deflects downward. At a current magnitude of 7 x 10-9 A, the spike train is a bit irregular, but continues for the duration of the current flow (A). At higher currents (B and C), the trains are regular and the frequency of discharge (spikes/sec) within the trains is proportional to the current magnitude. This kind of behavior is representative of most somata of mammalian neurons, though it is debated whether it is a property of the soma itself or the initial segment of the axon (the transition from soma to axon). For this discussion, we will treat the initial segment as part of the soma.
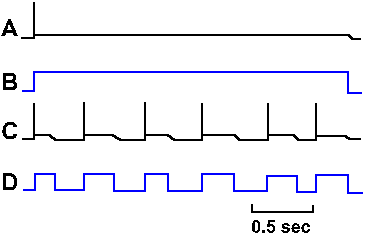 |
Fig. 3-31. Accommodation in the axon. A. Response of an axon to prolonged hypopolarizing current as shown in B. C. Response of the same axon to repeated short pulses of hypopolarizing current shown in D. |
How the sodium channels differ in these two types of membranes is unclear, but there is a clear difference in accommodation. There are different isoforms of the sodium channel; some are found in cell bodies, others in axons. Perhaps this difference reflects a difference in the isoform of the local channels. Actually, there is no reason for the axon to behave like the soma in response to prolonged outward currents, because axons probably never experience such currents. The axon is basically a follower; it follows what the soma (or initial segment) does. Its spikes are caused by the soma spikes by propagation as described earlier. (This is probably what George Bishop (Ann Rev Physiol 27: 1-8, 1965) had in mind when he said comically, "The axon doesn't think. It only ax.") The soma spikes generate fast current transients that recur with each spike and repeatedly initiate axon spikes as in Figure 3-30C. Axons, therefore, always generate trains of spikes identical in their timing (the spikes occur at the same times relative to each other) to those that occur in the soma. The soma, on the other hand, is the pacemaking or spike-generating region of the neuron, responsible for coding information it receives from other neurons (a property the soma shares with sensory receptors as we shall see in the next chapter). It experiences prolonged current flows (synaptic currents) and must respond to changes in current flow with changes in frequency of discharge. The soma's behavior, like that of the axon, is appropriate to its role in neural function.
The existence of different kinds of ionic channels in different densities in different regions of the neuron's membrane re-emphasizes that the fluidity of the lipid membrane is not unlimited. If it were so, then the dendrites would often have properties of axons, the somata often properties of dendrites, and so forth. In cases where an element external to the cell is involved, as at synapses, these elements may influence the aggregation of certain channels near them. Not every case involves an external element; in these other cases, some internal factor likely aggregates appropriate channels.
| Summary |
The membranes of excitable cells are composed of lipids and proteins organized into a fluid mosaic. It is the proteins that give different membranes their specific character. These proteins can sit on the membrane, they can be embedded in the surface of the membrane, or they can pass all the way through the membrane, and they can act as structural elements, pumps, channels, receptors, and enzymes. Membranes are permeable to small- and medium-sized lipid soluble molecules, but only small lipid insoluble molecules can pass through. The ease with which a molecule passes through depends upon its hydration radius and the characteristics of the channel through which it must pass. Nerve membranes have a high conductance for chloride and potassium ions, but a low conductance for sodium ions. The membrane has both resistance and capacitance, causing electrical signals applied to it to be greatly attenuated and badly distorted within a few millimeters of the site of application, i.e., it is a poor conductor of electricity. The time constant of the membrane ranges from 0.5-5.0 msec and the space constant is about 2 mm.
The membrane contains no metallic conductors, therefore any currents through the membrane must be carried by ions. Ions are not distributed equally on both the inside and outside of the membrane: sodium, calcium, and chloride concentrations are much higher outside than inside, potassium concentration is higher inside than outside, and the intracellular fluid contains some large anions that cannot leave the cell. Because of the differing concentrations of ions, there is always a tendency for ions to diffuse through the membrane. Differing concentrations of ions on two sides of a semi-permeable membrane (like the cell membrane) comprise a concentration cell or battery that creates electrical forces to counteract ion diffusion. There will be an equilibrium when concentration forces balance electrical forces, an electrochemical equilibrium. For each ion, electrochemical equilibrium occurs at its equilibrium potential. For chloride, the equilibrium potential is about -66 mV (for nerve, higher for muscle); for potassium, it is about -75 to -80 mV; and for sodium, it is about +55 to +60 mV, all expressed as voltage inside with respect to outside.
The resting membrane has a potential difference across it, called the resting membrane potential, that has a value of -50 to -90 mV depending upon the cell. This potential occurs because (1) the membrane is 20-30 times more permeable to chloride and potassium than to sodium; (2) chloride ions are able to redistribute themselves with changes in membrane potential and are thus at equilibrium; and (3) potassium ions cannot freely redistribute themselves because they must remain inside the cell to balance the electrical charge of the non-diffusible anions and maintain electrical neutrality. The value of the membrane potential depends upon the ratio of potassium conductance to sodium conductance. Because this ratio is usually very high, the membrane potential is usually near the potassium equilibrium potential. Thus, the membrane potential depends mainly upon the concentration gradient for potassium ions. The membrane is leaky, so that concentration gradients for sodium and potassium ions must be maintained by the sodium pump. The pump within a single neuron can be non-electrogenic, pumping equal numbers of sodium and potassium ions, or it can be electrogenic, generating a net outward current that may influence the value of the membrane potential. The pumping rate depends upon the intracellular sodium concentration.
When an excitable membrane is strongly stimulated, it generates an active response that is not predictable from the simple resistance-capacitance equivalent circuit. This response, called the action potential, is an initial rapid hypopolarization, a period of reversed polarization, and a rapid repolarization. The spike is triggered by hypopolarization of the membrane that leads to increased sodium conductance, inward current, and more hypopolarization until the sodium conductance is inactivated. The period of increasing sodium conductance accounts for the upstroke of the spike. The falling phase is produced by both sodium inactivation and a delayed increase in potassium conductance leading to an outward current and repolarization. A period of hyperpolarization following the spike is produced by a continued, heightened potassium conductance but a lower-than-normal sodium conductance. The spike does not occur in the absence of the sodium concentration gradient.
The spike, once initiated, travels down the axon because the inward current of the spike upstroke produces an electrotonic hypopolarization of the membrane in front of the spike. This hypopolarization is usually sufficient to bring the membrane to the critical firing level, and thus the spike propagates to the end of the axon. Conduction velocity increases if the diameter of the axon is increased and if the axon is myelinated. Myelination decreases the membrane time constant and increases the space constant of the membrane, thereby increasing the current density at the nodes and allowing the spike to jump from node to node.
Spike frequency is limited by the refractory periods that result from the sodium inactivation process and the fact that sodium channels are not available for re-activation for a short time after the membrane returns to the resting potential.
Ca2+ plays a role in stabilizing the membrane. Thus, as extracellular Ca2+ concentrations drop, the neuron becomes more excitable, whereas at very low concentrations it becomes completely inexcitable. In some neurons, Ca2+ takes the place of Na+ in generating the upstroke of the action potential. Usually, this occurs in dendrites or other places where rapid conduction over long distances is unnecessary.
The membrane is not the same all over a cell. Densities of voltage-gated channels are high in axons but usually lower in the soma and dendrites. Chemically gated channels are normally absent in axons but dense in the soma and dendrites. The behavior of channels also varies in different parts of a cell. In the axon, there is rapid adaptation, presumably due to accommodation, whereas in the soma adaptation is minimal. This difference reflects the role of the soma as pacemaker or spike generator and the axon as a simple follower-conductor.
| Suggested Reading |
- Catterall, WA: From ionic currents to molecular mechanisms: The structure and function of voltage-gated sodium channels. Neuron 26: 13-25, 2000.
- Cooke I, Lipkin M [eds]: Cellular Neurophysiology, New York, Holt, Rinehart, and Winston, 1972.
- Eccles JC: The Physiology of Nerve Cells. Baltimore, Johns Hopkins Press, 1968.
- Goldin, AL: Resurgence of sodium channel research. Ann Rev Physiol 63: 871-894, 2001.
- Guy HR, Seetharamulu P: Molecular model of the action potential sodium channel. Proc Nat Acad Sci 83: 508-512, 1986.
- Hagiwara S: Ca spike. Advan Biophys 4: 71-102, 1973.
- Hodgkin AL: The Conduction of the Nervous Impulse, Springfield IL, Thomas, 1964.
- Junge D: Nerve and Muscle Excitation, Sunderland MA, Sinauer, 1976.
- Katz S: Nerve, Muscle, and Synapse, New York, McGraw-Hill, 1966.
- Llinas R, Hess R: Tetrodotoxin-resistant dendritic spikes in avian Purkinje cells. Proc Nat Acad Sci 73: 2520-2523, 1976.
- Salzer, JL: Nodes of Ranvier come of age. Trends Neurosci 25: 2-5, 2002.
- Sigworth FJ: The patch clamp is more useful than anyone had expected. Fed Proceed 45:2673-2677, 1986.
- Stevens CF: The Neuron. Sci Amer 241: 55-65, 1979.
- Waxman SG: Integrative properties and design principles of axons. Int Rev Neurobiol 18: 1-40, 1975.
Footnotes
9. The term "depolarization" is used in most literature and textbooks for any hypopolarization. Though this is strictly incorrect, it is customary and widely accepted. Be warned!
10. Note: The amplification illustrated in Fig. 3-16 is less than that in Fig. 3-15 so the traces appear to be smaller. In fact, they would not be.
11. This should make sense if you recall that current entering a resistor makes that end of the resistor positive with respect to the other end. Thus, current passing inward through the membrane will make the outside more positive with respect to the inside (that's hyperpolarization), whereas current passing outward through the membrane will make the inside more positive with respect to the outside (that's hypopolarization).
12. According to fanciers of puffer fish, the fish are best when eating them makes the lips tingle. The sensation must be similar to that which occurs when novocaine begins to wear off following a trip to the dentist.
13. A change in conductance of 8 x 10-12 siemens would allow a Vm of 100 mV to drive a current of about 10-12 amperes through a channel. This amount of current would involve a movement of about 6000 Na+ ions.
14. This use of the term rectification by biophysicists is quite different from that of electrical engineers, meaning lower resistance to current flow in one direction than the other through a circuit element. Do not confuse these usages.
15. The inward current is carried by sodium ions as we have just seen, but it is not possible to say what ions carry the outward current. The most likely candidate would be K+.
[TOC] [Chapter 4] [Glossary] [Index] [Abbreviations]