
 Chapter 1
Chapter 1 
DIFFUSION AND TRANSPORT
This chapter deals with the processes by which substances move in
solutions, particularly how they move through cell membranes. There are
three basic processes for such movement:
- Simple diffusion (including a special case for water)
- Carrier-mediated transport
- Phagocytosis and pinocytosis
| Simple Diffusion |

|
Figure 1-1. Diffusion and diffusion potentials. A container, with a removable partition, contains water. Ordinary table salt, NaCl, is added to side 1 and then the partition is removed. After a time, NaCl is found in equal concentrations of both sides. |
![]() J = kC
J = kC![]() (1)
(1)
where k is a constant for a given temperature and C is the concentration in the compartment from which the flux is occurring.
In Figure 1-1, the side where the salt was put is numbered 1; the other side is numbered 2. Therefore, the flux from side 1 to side 2, J12 is:
![]() J12 = kC1
J12 = kC1![]() (2)
(2)
where C1 is the initial concentration of salt on side 1. As soon as some molecules have crossed the interface, the concentration on side 2 begins to increase, and there will be an increasing likelihood of a molecule recrossing the interface back to side 1. This probability is related to temperature and concentration--this time, to the concentration on side 2; the back flux, J21, is given by:
![]() J21 = kC2
J21 = kC2![]() (3)
(3)
The net movement or net flux, JN, between the two compartments at any time is simply the difference between the two one-way fluxes, J12, and J21,
![]() JN = J12 - J21 = kC1 - kC2 = k(C1 - C2)
JN = J12 - J21 = kC1 - kC2 = k(C1 - C2)![]() (4)
(4)
Diffusion is simply a net flux. The net flux is positive when C1 > C2, so the diffusion is from a region of higher concentration to a region of lower concentration, down the concentration gradient. The net flux is proportional to C1-C2, or proportional to the concentration difference between the two compartments.
Equilibrium is defined as the condition of no net flux, JN=0. When JN = 0, J21 = J12 in equation (4). Expressed in words, the equation means simply that the two one-way fluxes are equal at equilibrium, but neither flux need be zero. Even at equilibrium, molecules can move from one compartment to the other, but equal numbers must move in both directions. Only the net flux need be zero. (This condition is sometimes called a "dynamic equilibrium.") Equation 4 can be solved for JN = 0 as follows:
![]() 0 = JN = kC1 - kC2, or kC1 = kC2, or C1 = C2
0 = JN = kC1 - kC2, or kC1 = kC2, or C1 = C2![]() (5)
(5)
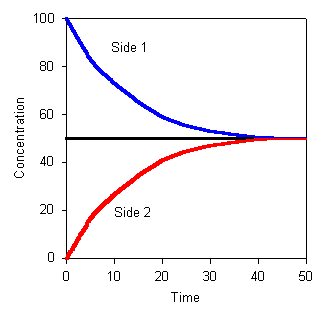 |
Figure 1-2. Changes in concentration on side 1 and side 2 with time. Note that concentrations are eventually the same, though the begin at different values. |
Thus, equilibrium will occur when the concentrations in the two compartments are equal. Until equilibrium is reached, there will be a net flux from side 1 to side 2 that is proportional to the concentration difference.
If we introduce a membrane, permeable to NaCl, between the compartments and repeat the experiment, the result will be the same. The net flux will be proportional to the difference in concentration between the two compartments with the constant of proportionality equal to the permeability coefficient, p, of the membrane for NaCl or JN = p(C1 - C2). The only real difference will be that the process occurs more slowly.
Diffusion speed
The speed of diffusion of a substance may be calculated from the equation:
![]() x2 = 2Dt
x2 = 2Dt
where x is the diffusion distance, t is the diffusion time and D is the diffusion coefficient. Taking a simple example will illustrate that diffusion is a slow process. Let D = 10-5 cm2/sec. Then we can calculate t for different values of x as shown in the following table:
| x | t |
| 1 micrometer | 0.5 msec |
| 100 micrometers | 5 sec |
| 1 cm | 14 hr |
Clearly, diffusion is rapid if the distance to the target is 1 micrometer or less; it is marginal if the distance is 100 micrometers. Many insects breathe through their skins, the air simply entering the cells directly. For them this is possible because they are small and the cells are located near a repository for air. Clearly, this mechanism would not work in a human. The distance from the skin surface to many organs is more than 1 cm, requiring an inordinately long time for gas exchange. A similar situation surrounds supplying nutrients to body tissues. Many of them are located more than 1 cm from the source of the nutrients. It is for this reason that we have lungs and a circulatory system.
Entry into cells
Lipid soluble substances can enter a cell by dissolving in the lipid portion of the membrane and diffusing through it. The greater the lipid solubility, the more readily a molecule will pass through the membrane, i.e., the greater will be the flux for a given concentration difference. The oil-water partition coefficient (solubility in oil/solubility in water) gives a useful measure of lipid solubility. Fig. 1-3 shows this relationship between permeability and partition coefficient for a number of different substances.
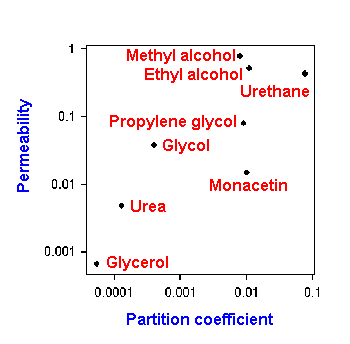 |
Figure 1-3. Oil/water partition coefficient plotted against membrane permeability for 8 different substances. |
Molecular size is not very important for lipid soluble molecules although very large ones enter cells a bit less readily. Examples of lipid soluble molecules that can pass through the membrane include: oxygen, carbon dioxide, steroid molecules, and anesthetic agents.
Water soluble, lipid-insoluble substances by definition cannot pass through membranes by dissolving in the lipids. How do they get through? There must be water-filled channels or pores spanning the membrane through which these substances may diffuse. These will admit substances up to about 200 Daltons in molecular weight, i.e., about the size of a glucose molecule. These pores are of different sizes, some as small as 4 Angstroms and as large as 8 Angstroms. Most substances cannot pass through pores because of their large size, especially when hydrated. The number of pores in an area of membrane is difficult to estimate, partly because they appear to be continuously recycled. Only 0.01% of a cell's membrane need be occupied by pores to account for the observed permeability.
Substances that can pass through these water-filled channels include: water, urea, some dissolved gases, and ions such as Na+, K+ and Ca2+. As we shall see, not all ions get through the membrane with equal ease. This is partly a function of the radius of hydration, but the structure of the channel also plays an important role.
Ion trapping
Diffusion of a substance depends only upon the concentrations of that substance. Thus, the presence of chloride in a solution of table salt, has no effect on the diffusion of sodium. Likewise, the presence of a metabolite of a substance or the ionic form of a substance has no effect on the diffusion of the substance itself. For example, glucose is metabolized to glucose-6-phosphate immediately upon entering a cell. The presence of this metabolite does not affect further diffusion of glucose.
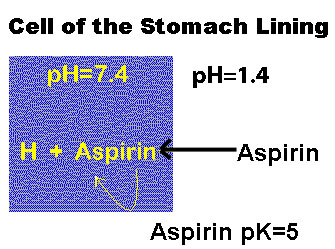 |
Figure 1-4. The phenomenon of ion trapping. The rectangle is supposed to indicate a cell in the stomach lining. Aspirin has a pK=5. At the higher pH inside the cell, aspirin ionizes and then cannot leave the cell. |
This property gives rise to a phenomenon known as ion trapping. Aspirin in the stomach, which has pH=1.4, exists mainly in the non-ionized (uncharged) form. In this form, it can enter the cells of the stomach lining. Once it enters the cells, which have pH=7.4, the aspirin is ionized because it has a pK=5, and, in this form, it cannot leave the cell. Ionized aspirin is not the same as non-ionized aspirin as far as diffusion is concerned. Therefore, the concentration of non-ionized aspirin inside the cell remains low, and it continues to enter the cell until it saturates and precipitates as crystals. These may actually rupture the mucosal cells and lead to gastric bleeding. One way to prevent this is drink a lot of water with aspirin in order to lower its concentration inside the stomach.
Ion trapping can be exploited for beneficial purposes as well. For example, aspirin poisoning can be treated by raising the pH of the urine to trap the ionized form there. It will be voided with the urine.
| Osmosis |
Water is a substance just like sodium or potassium or glucose. It will move down its concentration gradient by simple diffusion until equilibrium is reached, just like these other substances. In addition, water is subject to "osmosis," a bulk flow of molecules (like water moving through a tube). Diffusion of water comes about because of differences in water concentration; osmosis comes about because of differences in hydrostatic pressure. When both forces are present, the hydrostatic force will dominate. Diffusion of water has no effect upon the diffusion of other substances, but during osmosis, dissolved substances can get swept up in the stream of water and moved faster than would be expected from their diffusion alone. This is called "solvent drag."
Osmosis requires that the cell membrane be semi-permeable, meaning that not all substances can pass through it. The membrane must be permeable to water (all are), but it must be impermeable to some other substance. We will refer to particles that can pass through the membrane as "penetrating" and to those that cannot as "non-penetrating."
Pure water has a concentration of 55.5 moles/liter. Anything added to it lowers the water concentration. It is easier to express water concentration in terms of solute concentration, but all "osmotically active particles" must be considered. Thus, water concentration is expressed in osmoles, the number of moles of dissolved particles per liter of solution. A 1 M solution of glucose is, therefore, a 1 osmolar solution. Similarly, a 1 M solution of urea is a 1 osmolar solution. But, a 1 M solution of NaCl is a 2 osmolar solution because NaCl dissociates into two particles in solution. Furthermore, a 1 M solution of Na2SO4 is a 3 osmolar solution.
Bear in mind that the higher the osmolarity, the lower the water concentration. Therefore, water will move from regions of low osmotic concentration (high water concentration) to regions of high osmotic concentration (low water concentration).
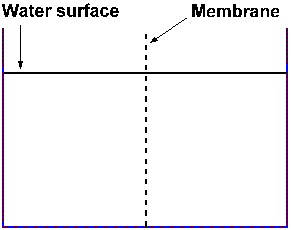 |
Figure 1-5a. Equal volumes of plain water in two compartments separated by a membrane (dashed line) |
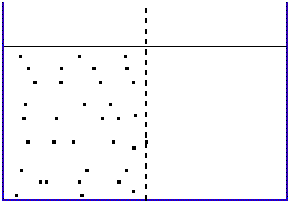 |
Figure 1-5b. Solute added only to the compartment on the left; membrane is impermeable to the solute |
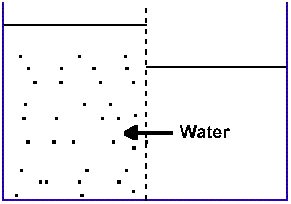 |
Figure 1-5c. With time the volume of the compartment on the left is seen to increase; that on the right is seen to decrease. |
Consider a container, divided into two compartments by a
semipermeable membrane through which water penetrates, but some solute
does not. This condition is shown in Figure 1-5a. Add some non-penetrating
solute to the left compartment (Figure 1-5b). Because the
solute dissolves completely, there will be essentially no change in
volume of the left compartment. After some time, the level of the water
in the right compartment will have fallen, that in the left will have
risen (Figure 1-5c). The only possible explanation for this occurrence is that water
has moved from right to left. This makes sense from what we know of
diffusion. Initially, the concentration of water on the right was 55.5
M or 100%, that on the left was something less than this value. Water
has diffused down its concentration gradient.
|
|
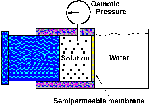
But, consider a different situation. Two chambers of a reservoir of water are separated by a semipermeable membrane as before. The left chamber contains some concentration of a non-penetrating solute and a piston that can move. As water enters the left chamber it pushes the piston to the left. You can see this in an animation by clicking the picture at the left. Note that the pressure gauge at the top of the left chamber does not change its reading--the force exerted by the increase in water is used to push the piston. If the piston is fixed, then it cannot move and the pressure measured by the gauge will increase. This pressure is called the osmotic pressure.
The osmotic pressure of a solution may be calculated from Van't Hoff's Law:
![]() P = iRTc
P = iRTc
where i is the number of ions formed by dissociation, R the ideal gas constant, T the absolute temperature and c the molar concentration. It can be seen that a 1 milliosmolar concentration difference will yield a 19 mmHg osmotic pressure.
Osmotic pressure is one of the parameters that determines whether water enters or leaves the blood in blood vessels. Some people use the term "oncotic pressure" or "colloidal osmotic pressure" in this application. The blood contains large protein molecules (e.g., albumin), which are non-penetrating. The greater their concentration, the greater will be the tendency for water to enter the capillaries.
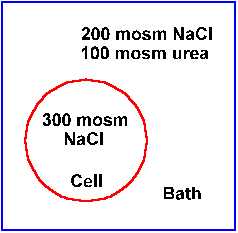 |
Figure 1-6. Cell found in a large bath. Components of the bath and cell are indicated. See text for discussion. |
Osmotic pressure is also a major determinant of the size or volume of individual cells. A cell placed in solution may change size depending upon what is in the solution. Obviously, a physician does not want to change the size of cells in a patient's body. Therefore, it is important to exercise care when administering fluids to a patient.
A solution whose osmotic concentration is greater than that of cytoplasm is called an hyperosmotic solution. A solution whose concentration is less than that of cytoplasm is called an hyposmotic solution. The final possibility is an isosmotic solution. Just knowing the osmolarity of a solution is not sufficient to determine what will happen to cells. Consider the situation illustrated in Figure 1-6. The osmotic concentration of the cell's cytoplasm is 300 milliosmoles/liter. The osmotic concentration of the solution into which it was placed is also 300 milliosmoles/liter, 200 from NaCl and 100 from urea. With equal osmotic concentrations and, therefore, equal water concentrations, you might think that the cell would stay the same size--water would neither enter nor leave.
However, urea is a penetrating particle; it easily enters and leaves cells. For living cells, NaCl is non-penetrating because of the sodium pump (chloride follows sodium to preserve electrical neutrality). The urea will enter the cell down its concentration gradient and carry water with it. That will cause the cell to swell.
It is obvious that osmolarity does not indicate uniquely what will happen to cell volume in solution. A different terminology gives us that unique determination. An isotonic solution is one in which a cell will neither shrink nor swell, an hypertonic solution is one in which a cell will shrink, and an hypotonic solution is one in which a cell will swell. Obviously, osmolarity depends only upon the number of particles in solution, whereas tonicity depends both upon the number of particles and whether or not they penetrate the membrane. Bear in mind that a solution of only penetrating particles will effect no change in volume of a cell.
| Carrier Mediated Transport |
Properties of carrier mediated transport
This is a category of processes that accounts for passage through the membrane of large, lipid-insoluble molecules and ions. All use carrier systems, i.e., special carrier molecules are required to be present in the membrane to help in the movement of the transported molecules. These carrier systems all show three properties: specificity, saturation and competition.
By specificity, we mean that only certain molecules are transported by the system. For example, the transport system that moves glucose works only for the D-isomer not for the L-isomer, and it doesn't work for other sugars.
Because there are a limited number of special carrier molecules in the membrane, only that number of transported molecules can be accommodated at one time. Having more present does not increase the rate of transport. That can be seen in Figure 1-7. For simple diffusion, as concentration increases so does the rate of diffusion, and the relationship is linear (black line, A). However, with mediated transport, the rate of diffusion increases as concentration increases up to a point, and then there is no further increase in rate with increasing concentration (red (B) and blue (C) curves). At this point, we say the system is saturated. Presumably, all of the carrier molecules are being used.
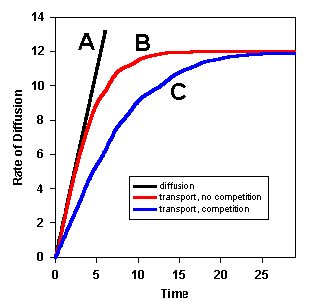 |
Figure 1-7. The rate of movement of a substance through a cell membrane by simple and membrane transport, with and without competition. The rate of movement by simple diffusion is linear, that for transport is clearly nonlinear with a plateau. In the presence of a competitor for the same carrier, the rate of transport is slowed. |
A physical example may help to visualize this property. Suppose 75,000 people want to get into Memorial Stadium to watch a football game. If there is an unlimited number of entry doors, then all of the people can enter at the same time--the rate is maximum. If you have been there, you know that there is a limited number of doors, and the rate is quite a bit less than maximum.
When two or more substances use the same carrier molecule, then the presence of one will slow the rate of transport of the another. They compete for the use of the carrier molecules. This is another obvious consequence of a limited number of carrier molecules, and it is called competition. This phenomenon is also shown in Figure 1-7. With competition (blue curve, C) the rate is slower than without (red curve, B).
This process behaves much like simple diffusion in that net transport occurs down the concentration gradient for the transported substance. Because it occurs downhill, no external energy is required; the energy required by facilitated diffusion comes from the same source as that for simple diffusion--thermal motion. As in simple diffusion, there is an equilibrium condition for facilitated diffusion. There will be no net transport when the concentrations on the two sides of the membrane are equal.
Glucose can get through the membrane by diffusing through the pores (its diameter is approximately that of the largest ones), but the rate at which it enters most cells is higher than one would expect for diffusion. For most cells, most of the glucose enters by facilitated diffusion. Once glucose enters the cell it is immediately metabolized to glucose-6-phosphate. So, the intracellular concentration of glucose is always near zero. Thus, there is a continuous gradient toward the inside of the cell, and the facilitated diffusion system will always bring glucose into the cell. However, if we artificially raise the glucose concentration within the cell above that outside the cell and prevent it from being metabolized, then the facilitated diffusion system will take glucose out of the cell. Thus, the direction of transport is determined by the concentration gradient, not by some property of the transport system itself.
|
|
Presumably, the carrier molecule is more likely to attach to the transported molecule where that molecule is in highest concentration. Once the two are attached, a conformational change in the carrier molecule exposes the transported molecule to the inside of the cell, where it is released because of its lower concentration. At least, that is one model of how the process works. To see an animation of the process, click on the picture to the right.
Glucose enters most cells by facilitated diffusion. In addition, amino acids and sometimes sodium ions are transported by this mechanism.
Sometimes molecules must enter or leave a cell even though they are in higher concentration at their destination. Sodium ions, for example, are continuously "pumped" out of all cells, though their concentration is ten times higher outside. We have seen that under these conditions sodium ions have a natural tendency to enter the cells by diffusion down their concentration gradient. Therefore, to move them out of the cell requires expenditure of energy. A form of equilibrium also applies to active transport. When the concentration increases to the point that particles "leak" into the cell at the same rate that they are pumped out by the active transport system, a steady state or equilibrium condition will exist.
Such active transport systems or "pumps," as they are often called, probably only transport ions--charged particles. As we shall see, uncharged particles may move by coupling with the ions being transported. Some pumps are capable of moving more than one ion at a time. In Chapter 3, we will see that the sodium-potassium pump moves sodium out of the cell and potassium into the cell at the same time.
Pumps can be electrogenic or non-electrogenic, depending upon the number of charges transported in each direction across the cell membrane. For example, if the sodium pump were to pump more sodium ions out of the cell than it pumps potassium ions in, there would be a net outward current. This current, through resting membrane, would slightly hypopolarize the cell membrane (electrogenic). Conversely, if the same number of sodium and potassium ions were pumped, then there would be no net current and no change in membrane potential (non-electrogenic).
|
|
One model of the active transport process has the carrier molecule with a higher affinity for sodium ions on the inside of the cell. Attachment of a sodium ion causes a conformational change in the carrier molecule, exposing the sodium ion to the outside of the cell, where the affinity of the carrier molecule for sodium is smaller, and the sodium is released. You can click on the picture at the right to see an animation of this model for a general case.
| Co-Transport |
When a substance moves from a region of higher concentration to a region of lower concentration, as it does during diffusion, it gives back the energy that was supplied to create the concentration gradient in the first place. That energy can be used to move other substances, even up their concentration gradients. This is the essence of co-transport or ion-coupled transport.
In a symport, the two substances being transported move in the same direction across the membrane. In the intestine, sodium ions diffuse into the lining cells by diffusion along the normal outside-to-inside gradient. There is a carrier system in the cell membrane which couples this movement to an inward movement of glucose molecules. Glucose could not be transported actively because it has no charge, but it can move by this process, even up its concentration gradient. It is for this reason, that there is normally no glucose in the feces--it all gets removed by this symport.
This process does not require external energy. The sodium pump can be poisoned, and it will still continue as long as a sodium concentration gradient remains. However, some gradient must be present; so the entering sodium must be removed from the cells. Apparently, sodium pumps in these luminal cells are sequestered to the blood side of the cells; all entering sodium is pumped out of the cells into the blood, not back into the intestinal lumen. Glucose is removed from the cell by facilitated diffusion, and water follows along with both sodium and glucose in order to keep its concentrations in equilibrium (see osmosis earlier in this chapter).
A similar mechanism can exchange substances across membranes. Several substances are known to be exchanged for sodium ions. In all cells, there exists a H+-Na+ antiport. In cardiac muscle, there is a Ca2+-Na+ antiport. The latter is blocked by both digoxin and ouabain, which are known to inhibit ATPase activity. When the antiport is blocked, calcium concentration rises within the cells, strengthening the force of contraction.
Antiports do not have to involve sodium ions. In erythrocytes and elsewhere, there exists a Cl--HCO3- antiport. Presumably, this plays some role in buffering within the cells that have it.
| Phagocytosis and pinocytosis |
Sometimes water-soluble substances too large to pass through the pores must get into or out of cells. In addition, there are times when the contents of vesicles must be released all at once. These take a special mechanism.
Exocytosis
|
|
During exocytosis, a substance is relased from the cell. When a substance is to be released, for example, during synaptic transmission (the communication between two nerve cells), the substance is usually stored within a secretory vesicle. The release process involves migration of the vesicle to the cell membrane, fusion of the vesicle membrane with the cell membrane, and rupture of the point of junction. The substance contained within the vesicle then finds itself within the extracellular fluid. An animation of this process may be seen by clicking on the picture at the right.
Endocytosis

|
|
To take a substance into the cell, the process is simply played out in reverse, and it is called endocytosis. The substance moves to the cell membrane or the cell moves to the substance. A portion of the membrane surrounds the substance, and the substance containing portion "pinches" off to form an intracellular vesicle. This special mechanism is called phagocytosis or pinocytosis, which translate to "cell eating" and "cell drinking." The former is applied to movement of particulate material, the latter to fluids.
An animation of the process may be viewed by clicking the picture at the right. Note that in exocytosis the vesicular membrane actually becomes a part of the cell membrane. Conversely, in endocytosis a portion of the cell membrane is lost in formation of a vesicle. In this way, the cell membrane is constantly turning over. Clearly, there must be a balance between endocytosis, exocytosis--the formation of new membrane and the degradation of old membrane--if the cell is to maintain its size.